4 蒙特卡洛方法

数学分析（mathematical analysis）是数学中与极限及其相关理论有关的一个古老的分支，这些相关理论包括微积分，测度论，极限和解析函数等。数学分析研究内容包括实数，复数，实函数以及复变函数，它是由微积分演进而来，在微积分发展至现代阶段中，从应用中的方法总结升华为一类综合性的分析方法。

通常我们使用解析方法（analytic methods）来对这些问题进行分析，在此方法下可以得到确定性的解析解。然而在许多实际问题中，精确值往往无法求得，例如具有无限维度被积函数的积分，具有无限不循环小数部分的无理数等，因此使用近似的数值分析（numerical analysis）方法应运而生，数值分析方法的目的不在于求出正确的答案，而是在一个合理误差范围的条件下找到近似解。例如插值法，回归分析法以及本书后面的章节会讨论的迭代法等等。

蒙特卡洛方法（Monte Carlo method）是数值分析中的一个重要分支，它的核心概念是使用随机性来解决确定性的问题。大数定律告诉我们，对于满足某个概率分布的随机变量，其数学期望所描述的积分可以使用这个随机变量随机采样的样本均值来近似，因此在一定的误差范围内，我们能够使用大量的随机数来近似积分运算的结果，例如在图（1）中，分布函数$f(x)=x^2+y^2$在区间$[0,1]^2$上的积分为$\cfrac{\pi}{4}$，因此可以在该区间内产生大量均匀分布的随机数，随着随机数数量的增加，落在圆内随机数数量的比例值将逼近$\cfrac{\pi}{4}$的值，以此方法便可以计算出$\pi$近似值（后面将证明，这个误差范围和随机数的数量有关）。

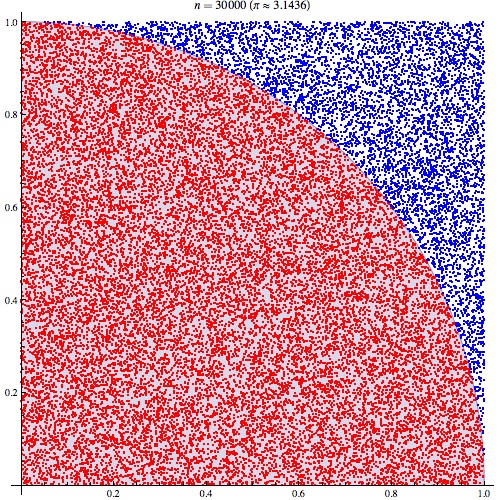
图1：使用蒙特卡洛方法来计算$\pi$的值，这里使用30000个随机点，其$\pi$的估计值的误差范围在0.07%以内（图片来自Wikipedia[CaitlinJo]）

蒙特卡洛方法的起源可以上溯到18世纪，法国数学家蒲丰为了验证大数定律，提出使用随机投针实验来估算圆周率$\pi$的值，该实验初步演示了蒙特卡洛方法的随机采样和统计估计的模拟思想。然而由于缺乏高速计算工具，没有现代电子计算机，不可能进行千百万次的模拟计算，由于技术条件不成熟，蒙特卡洛方法经历了近两个世纪漫长的启蒙时期。

现代形式的蒙特卡洛方法最早是由斯塔尼斯拉夫·乌拉姆（Stanislaw Ulam）于20世纪40年代晚期，在洛斯阿拉莫斯国家实验室进行核武器研究时提出，当时在核武器的研制过程中涉及中子在结构复杂的原子弹内扩散和增值的问题，需要求解高维玻尔兹曼方程，这是一个高维偏微分积分方程，无法使用解析方法求解；跟随着乌拉姆的突破性工作，计算机科学家约翰·冯·诺伊曼（John von Neumann）立即明白了它的重要意义，并把它编程实现在世界上第一台电子计算机ENIAC上；随后于1953年，尼古拉斯·梅特罗波利斯（Nicholas Metropolis）与其他四位科学家提出了著名的梅特罗波利斯算法[cite a:EquationofStateCalculationsbyFastComputingMachines]，该算法对近代工业和科技发展产生了非常重要的影响，其甚至被称为20世纪最重要的算法。

蒙特卡洛方法被广泛运用于现代科技和工业中，它主要被应用于最优化理论，数值积分方法以及从概率分布函数中产生随机数等领域和方面。在计算机图形学中，蒙特卡洛方法主要被应用于物理模拟以及光照传输中的积分运算，从后面第5章即将介绍的渲染方程的路径积分形式中可以看到，其被积函数是一个具有无限维度的高维函数，在离线渲染领域，渲染方程几乎只能使用蒙特卡洛方法来进行计算。

本章首先复习概率论相关的一些基础知识和概念，例如随机变量，方差，数学期望等，然后由大数定律推导出蒙特卡洛积分形式；紧接着讨论怎样对已知分布函数进行随机数取样，这包括逆变换算法，取舍算法，复合算法以及基于马尔可夫链（Markov Chain）的梅特罗波利斯算法（Metropolis algorithm）；由于蒙特卡洛方法都存在一定范围的误差，所以最后我们讨论一些有效的减少蒙特卡洛模拟方差的方法，例如重要性采样，以及基于数论的拟蒙特卡洛方法（Quasi-Monte Carlo method）等。本章讨论的内容是后面路径追踪，光子映射等全局光照算法的重要基础知识和工具。