3.3.2 分簇着色

为了进一步剔除光照计算阶段每个像素点受影响的光源数量，分簇着色[a:ClusteredDeferredandForwardShading]（clustered shading）在分块着色的基础上将像素分组的划分从2D的屏幕空间（screen space）延伸到3D的观察空间（view space），与之相应，每个3D的块称为一个簇（cluster），从而使每个光源真正做到仅影响其局部区域。

分簇着色的基本步骤如下：

1. 将几何场景渲染到G-buffer以获取有效可视表面点及其相关材质属性。
2. 计算每个簇的索引键值（cluster key），也称为簇分配。
3. 找出唯一的簇集合。
4. 分配光源到每个簇。
5. 利用每个簇的光源列表对像素点进行着色计算。

其中第一步和传统的延迟着色或分块着色并没有什么区别；第二步对每个像素点执行一次计算，它根据像素点的位置（也可以加入法线的限制）计算出每个像素点的的簇索引键值；然后第三步将这些簇索引键值合并，以形成一个包含唯一键值的簇列表；第四步则将光源分配到每个簇；最后第五步根据每个像素所在簇的光源列表对像素点进行着色。

簇分配

对3D空间执行某种空间结构的划分，都可能导致大量的空域，比如场景中会有大量空间位置不包含最终屏幕上呈现的像素点。传统的几何空间的划分可以使用如BVH这样的树状结构来忽略大部分空域，但是分簇着色使用的是一种特殊的子空间结构（见下面的内容），并不能简单地用树状结构进行管理。所以分簇着色使用一种特殊的方式来构建簇集合：它对每个可视像素点都做一个簇索引键值的计算，这样遍历完所有像素点后的簇索引键值就是有效的簇，然后去掉重复的（即一个簇内的像素点计算出相同的索引值）簇索引键值，就形成一个有效的簇列表。

簇分配的第一个问题涉及怎样表述每一个簇的空间结构，因为这关系到簇索引键值怎样计算，一般的按一个固定尺寸的正方体（uniform grid）的划分会导致离摄像机较远的区域拥有非常密集的簇，所以其簇的密度几乎接近于像素的大小，这显然增加了后面光源分配的计算量；考虑到我们仅仅对视锥体内的点感兴趣，即观察空间（view space），所以分簇着色技术对视锥体进行划分，它以分块着色中2D屏幕上块的划分为基础，然后在深度方向上添加一个细分维度，如图（1）所示，这样划分的每个子空间称为一个簇（cluster），或者子视椎体（sub frustum），或者视锥体素（frustum voxel，froxel（这是一个来自[a:Learningfromfailure]中的概念。））。

图（1）：分簇着色使用的是一种针对视锥体空间进行划分的方法，它以分块着色的块为基础，在深度方向上按指数形式进行划分，每个子空间称为一个簇，左图仅列出屏幕空间Y方向

由于经过摄像机的透视投影，同样大小的物体在更远的在屏幕上所占的空间更小，所以分簇着色没有在深度方向上使用平均长度划分，而是以指数的形式划分深度方向，即更远的地方簇的尺寸更大，更近的地方簇的尺寸更小，如图（1）所示，这样每个簇的尺寸更接近于一个立方体。

那么，怎样通过一个屏幕坐标系的像素点位置计算出该像素点所在的簇的索引键值呢？假设在屏幕空间Y方向细分子空间（在屏幕空间每个块的大小为$32\times 32$像素）的数量为$S_y$，则深度方向上第$k$个子视锥体（注意这里指的是包含第$k$层上所有的簇子椎体，如图（1）左边顶部的虚线所指示的部分。）的近平面$near_k$在Y方向的长度为：

$$near_k=near_{k-1}+h_{k_1}$$

（式1）

对于第一个子视锥体，$near_0=near$（$near$表示整个摄像机视锥体的近平面Y方向上的长度），对于一个$2\theta$的张角，有以下关系：

$$h_0=\frac{2near\tan{\theta}}{S_y}$$

（式2）

其中，$h_k$表示第$k$级子视锥体上每个簇在Y方向的长度，由此可以得出：

$$near_k=near(1+\frac{2\tan{\theta}}{S_y})^k$$

（式3）

由于每个簇在深度方向上的长度：$d_k=h_k$，如图（1）所示，则解出$k$的值为：

$$k=\Bigg\lfloor \frac{\log{(-z_{vs}/near)}}{\log{(1+\frac{2\tan{\theta}}{S_y})}} \Bigg\rfloor$$

（式4）

这里${\rm floor}(x)=\lfloor x\rfloor$称为一个下取整函数（floor function），它表示取小于或等于$x$的最大整数，对于的上取整函数（ceiling function）为${\rm ceiling}(x)\lceil x\rceil$表示取大于或等于$x$的最小整数。

利用上式我们便可以计算出一个用三元组$(i,j,k)$表示的簇索引键值，假设$(x_{ss},y_{ss})$表示像素点在屏幕空间（screen space）的坐标，$(t_x,t_y)$分别表示屏幕空间每个块的尺寸，则$(i,j)=(\lfloor x_{ss}/tx\rfloor,\lfloor y_{ss}/t_y\rfloor)$；$z_{vs}$表示观察空间（view space）的深度值。

所以，给定一个像素点的坐标，我们便可以计算出该像素点所在簇的索引键值，这个索引键值由$(i,j,k)$三元组表示。在[a:ClusteredDeferredandForwardShading]的实现中，他们为$i,j$分量分别分配8位，而$k$分量分配10位，所以总共需要26位的长度来表示一个簇索引键值。

分簇着色中簇的索引值键值并没限定只能使用空间坐标来表示，它还可以使用更高的维度来使光源分配的数量更接近实际有效的光源数量。在[a:ClusteredDeferredandForwardShading]中还可以为一个簇指定该簇内像素点的法线分布，从而可以有效地进行背面剔除（back-face culling）。为此，它们为索引键值增加了6位用来表示法线分布，这样簇的索引键值就变成32位，可以使用一个32位的颜色值表示，其中包含$(i,j,k,normal)$四个分量。

为了使用有限的数据长度表示法线的空间分布，他们使用一个假想的立方体来表示空间分布，6位数据长度可以用来表示64个位的组合，所以立方体可以被细分为$3\times 3$个的子立方体，每个面的每个立方体分别表示一个锥型（cone）（为了计算简便，这里不会表述严格的法线空间分布，而仅仅是用每个子立方体代表一个锥形范围，如果包含多个子立方体方向，则将它们合并为更大范围的锥形，这样实际是夸大了法线分布的范围，但是这对于光源密集的区域，存在背面剔除的光源的数量还是很大的，大部分表面的法线分布都在一个很小的范围内。）的空间范围，这样一共需要$3\times 3\times 6=54$个位组合，如图（2）左边所示。

图（2）：每个簇内像素的法线分布用一个$3\times 3$的立方体表示，立方体每个面的每个细分面表示一个锥形的法线分布范围，54个位的组合可以由每个像素点分别计算出来

当法线分别被提供之后，表面背面的光源可以进一步被剔除（利用法线分布来剔除背面的光源，在Battlefield 3中又称为法线剔除（normal culling）。如果入射光方向（从光源到簇中心位置的方向）与法线锥形的中心轴之间的夹角$\omega$大于$\pi /2+\alpha+\delta$，则该光源应该被剔除。这里$\alpha$是法线锥形的半角（half angle），$\delta$是从光源发出的包围簇的AABB包围盒的锥形的半角，如图（2）右边所示。

找出唯一的簇集合

当每个像素点所在的簇索引键值被计算出来以后，形成一个包含重复键值的簇索引键值列表，这时我们需要压缩该列表，去除重复的部分（同一个簇内的所有像素点拥有相同的簇索引键值），以形成一个包含唯一簇索引键值的簇列表，如图（3）所示。

由于2D屏幕空间相邻像素点所在的簇在3D观察空间上并不一定是连续的（例如由于表面不连续导致两个像素点在深度方向上的距离很远，此时虽然它们在2D的屏幕空间相邻，但是所在的簇并不相邻。），所以这些由像素点计算出的簇索引键值也并不一定是连续的，如图（3）上图。因此要想去除重复键值，最简单的方法就是首先对索引键值列表进行排序，如图（3）中间小图，然后去除掉每一段重复的索引键值即可，如图（3）下图。

图（3）：对索引键值列表进行排序和压缩，以找到唯一的索引键值，索引键值的排序可以基于深度或者法线方向等。

然而在GPU中进行排序是一件非常影响性能的事情，[a:ClusteredDeferredandForwardShading]的做法是首先以2D屏幕空间的块为单位进行本地排序，由于每个块内的像素点是连续的，并且它是$32\times 32$大小的像素块，所以可以充分利用GPU的并行计算性能，并且每个块内的数据可以写入到本地共享缓存，而不是全局内存进行计算。

另一种方法是使用虚拟纹理[a:VirtualTexturing]（virtual texture），虚拟纹理用来存储需要巨大内存的稀疏数据，它可以将一个地址映射到一片紧密的内存区，这样用来降低内存的占用，虚拟内存使用页表（page table）来映射索引到紧密的物理内存区。然而由于簇索引键值的可能值的范围非常巨大，所以他们使用[a:Glift:GenericEfficientRandom-AccessGPUDataStructures]中的动态分配页表的方法来节省更多的空间，感兴趣的读者可以进一步参考这些论文信息。

分配光源到簇

传统的簇光源分配方法是遍历每个簇，然后对每个簇遍历每个光源，进行每光源$-$簇之间的AABB的包围盒相交测试。在这个基础上，[a:ClusteredDeferredandForwardShading]提出首先对所有光源构建一个包围体层次结构（bounding volume hierarchy，BVH），以此来加速每个簇内光源的遍历。[a:PracticalClusteredShading]进一步提供了一些加速点光源和聚光灯光源与簇的相交计算，这通过进一步挖掘光源的真实包围几何体而不是一个简单的立方体包围体来减少簇的计算量。

本节我们要介绍的是来自[a:GPUPro7:AdvancedRenderingTechniques]中针对DirectX 12的基于保守光栅化技术的光源分配方法，这是一种利用图形处理器的光栅化技术能够产生非常精确的簇光源分配的方法，当然这种方法仅适用于凸面光源（convex light）形状，考虑到大多数光源如点光源和聚光灯光源的包围体都是凸面的，因此这种方法非常实用。

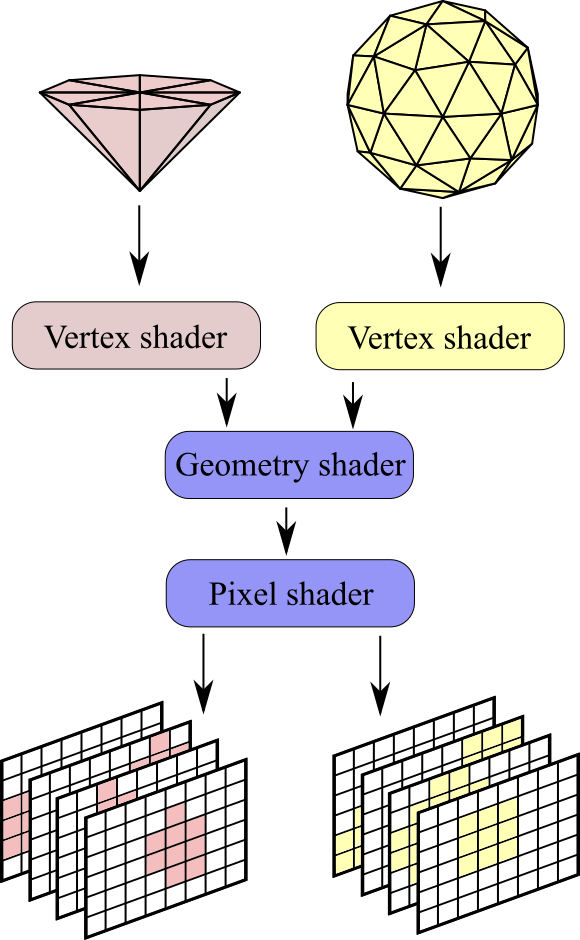
保守光栅化（conservative rasterization）的概念非常简单，传统光栅化技术在选择每个图元所覆盖的片元时，是以该图元所占的面积是否覆盖该片元的中心位置来决定该图元是否覆盖到该片元，如图（4）(a)图所示，显然这样的方法运用到光源剔除中就会漏掉一部分光源对簇的影响。与之相对应，保守光栅化则考虑任何部分被图元面积占用的片元均为有效片元，如图（4）(b)图所示。在DirectX 12中，通过在创建一个管线状态对象的时候设置ConservativeRaster的标识为D3D12_CONSERVATIVE_RASTERIZATION_MODE_ON来开启保守光栅化（OpenGL也可以通过一些扩展如GL_INTEL_conservative_rasterization和GL_NV_conservative_raster等来支持保守光栅化。）。

图（4）：传统光栅化与保守光栅化的区别，保守光栅化会包含所有图元面积覆盖到任何部分面积的片元

保守光栅化簇光源分配方法的基本过程可以分为两步，这两步均针对每个光源类型为单位进行：

1. 壳通道（shell pass）: 此通道首先将每个光源的包围几何体利用光栅化技术渲染到2D屏幕上以块（tile）为基本单位的分辨率上，并记下每个光源在每个块上的最大和最小深度值。之所以称为壳通道，是因为它找出了每个光源在每个块所在的子视锥体上所占的外形；
2. 填充通道（fill pass）： 利用壳通道产生的最大最小深度值来填充簇的光源列表。

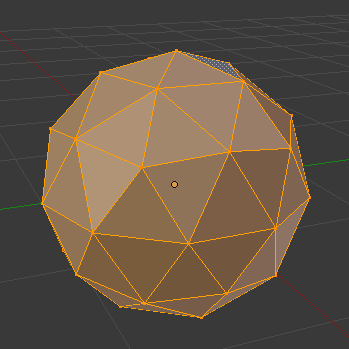
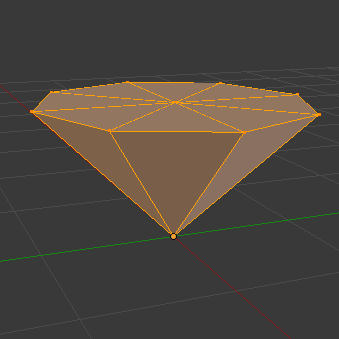
图（5）：在保守光栅化光源分配技术中，每个类型的光源使用一个单位网格表述，它们可以在每个实例中使用不同的变换矩阵改变尺寸和位置

由于使用光栅化技术，所以每个光源必须要有一个网格的几何表述，并且该几何表述必须是凸面的，这种几何表述也使得我们可以使用一些不规则的光源类型。需要注意的是，由于场景中的光源数量比较大，所以分别对每个特定的光源实例存储对应的几何数据并不是一个好方法，所以这里仅对每个类型的光源存储一个几何网格数据，并且每个顶点数据在$x-,y-$和$z-$方向上分布被限制到$-1$到1的单位尺寸，如图（5）所示，这样就可以使用图形接口中的实例化渲染，而每个渲染实例在顶点着色器中被变换到其光源的真实尺寸及位置。所以在保守光栅化光源分配方法中，每个通道都是以一个光源类型（而不是每个光源实例）为单位的。

壳通道

壳通道的主要任务是找出每个光源在屏幕上每个块（tile）内包围簇范围的最大最小深度，例如图（5）所示，由于光源始终是凸面的，只要找出这两个值，则在后面的填充通道则很容易正确地分配每个光源到每个簇内。由于深度方向上簇的数量有限，所有一个R8G8的渲染目标足以存储两个簇的深度值。

图（5）：壳通道的主要任务是找出每个光源在每个块内覆盖的簇的范围，由于光源是凸面的，所有找出最大最小深度方向上的簇之后，该光源就会被分配到该块内最大和最小深度范围以内的所有簇中去

要存储每个光源在每个块上的最大最小深度值，就需要为每个光源设置一个独立的渲染目标，而前面我们已经说明每个通道是以光源类型为单位的，每个光源类型包含多个光源的实例，所以这就要求渲染目标是一个Texture2DArray类型的数组纹理，其数组的数量为每个类型光源对应的光源实例，数组中每个图像的分辨率等于2D屏幕上块的分辨率，如图（6）所示。

图（6）：保守光栅化光源分配方法以光源类型为绘制单位，图中左右两列分别表示聚光灯和点光源两个不同的类型；每个类型的每个光源实例都对应一个渲染目标，所以下边的渲染目标是一个数组纹理，数组纹理的尺寸对应该类型光源实例的数量，每个纹理的分辨率为2D屏幕上块的分辨率；每个光源实例对应的纹理切片的渲染目标在几何着色器中选择

每个光源类型的所有光源实例通过DrawIndexedInstanced实例化渲染命令开始壳通道的绘制，实例的数量则等于场景中该光源类型光源实例的数量，每个光源实例拥有自己的变换矩阵用于将单位网格顶点数据变换到视图空间，顶点着色器根据SV_InstanceID来分别对每个光源实例的顶点执行变换。

在保守光栅化光源分配方法中，几何着色器必须被使用以设置每个实例的光源被渲染到不同渲染目标中，这通过在几何着色器中设置SV_RenderTarget\ ArrayIndex到数组纹理中不同的切片来实现。此外，为了后面片元着色器的正确处理，每个片元需要与一个三角形图形进行比较，所以我们需要将三角形的三个顶点输入到片元着色器，同时标识这些顶点变量为nointerpolation，以保证片元着色器中对簇深度的所有计算都是在观察空间的，这是因为有些光源处于视锥体之外的仍要被考虑（例如部分与视锥体相交），如果使用屏幕空间则这部分光源不能够被正确表述。

片元着色器的每个实例对应于屏幕区域一个块，每个块实际上是一个以摄像机为原点，四个面分别穿过块四边的锥形。一旦一个片元着色器实例被执行，说明三角形的至少一部分和该块相交，所以在片元着色器中每个三角形必须与该块对应的锥形进行相交计算。块与三角形进行相交计算时，最大最小深度可能的值的情况如图（7）所示，圆圈表示最大最小深度值出现的地方，这里算法比较简单，读者可以参考[a:GPUPro7:AdvancedRenderingTechniques]中的算法实现，这里仅讨论思路。

图（7）：块与三角形相交的三种可能的情况，其中(a)发生于三角形的边上，(b)出现在块的四个角，而(c)出现于三角形的三个顶点

相交计算出的结果根据该三角形面的方向以确定是最大深度或最小深度值，这些深度值在根据簇在深度方向上的指数分布或其他特征求出该簇的索引值（注意这里的簇索引值可能尽是深度方向上的索引，而不需要存储全局的索引值，这样能够使用更少的数据进行存储，否则16位的R8G8渲染目标根据存储不了全局那么多的簇索引值，后续的填充通道再将其转化为全局簇索引值。），然后将这两个值写入到该光源实例对应的渲染目标上。

填充通道

有了每个光源在每个块内的最大最小深度值，填充通道直接使用一个计算着色器，它同样以每个光源类型为单位，以块为分辨率，分别根据每个块内每个光源所占的最大最小深度值对其他介于最大最小深度之间的簇进行填充，如图（8）所示，每个计算着色器实例内遍历该实例对应块内所有的簇，只要簇索引值介于最大最小值值之间则对其进行光源分配，这里需要注意的是最大最小值存储的是深度方向的簇索引值，所以需要进行正确地转换。这里计算出的结果将被直接写入到全局的簇光源索引值列表中去，这和分块着色的思路差不多。

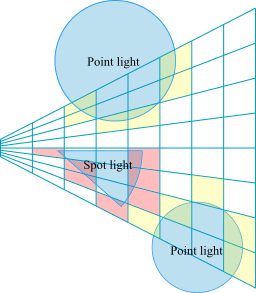
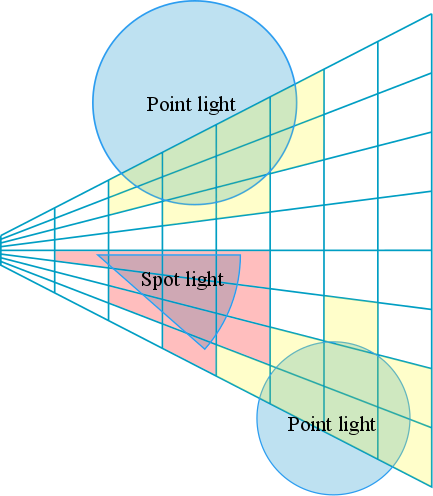
图（8）：壳通道计算出每个光源在每个块内的最大最小深度值，填充通道就可以利用两个值对每个簇进行光源分配，基于保守光栅化的光源分配方法非常能够非常精确地反应光源的实际几何形状，大大减少了无效的光源分配

着色计算

分簇着色和分块着色方法在着色计算方面没有太多区别，它同样可以使用于前向或延迟渲染方法中。但由于大大减少了每个簇内光源的数量，因此渲染性能较分块着色得到很大提升，如图（9）所示。

图（9）：图中的颜色表示光源数量，分块着色（上图）和分簇着色（下图）从屏幕的块看上去的光源数量呈现较大的差别，分块着色存在大量的无效光源

分簇着色更进一步地利用光源的局部性，将每个光源对环境的影响降到最低，从而提供更好的计算性能，从图（9）我们可以看到分簇着色每个像素计算的光照数量非常低，从而能够轻松应付巨大的光源数量，因为不管光源数量多么巨大，分配到每个簇内的光源数量几乎没有太多变化（通常场景中的光源都是大致平均分配到整个场景中，现实中很少那种很多光源堆积到一个局部空间的情况。），这只是存在光源分配阶段由于光源数量的增多导致的计算量，因为在整个计算中，只有光源分配部分是和光源数量有较大耦合的。

分簇着色最重大的意义在于，通过这种光源的局部性特征，将场景复杂度完全从光源数量中解脱出来，从而不管场景变得多么复杂，它能始终提供一个稳定的帧率，这是实时渲染技术最重要的权衡指标，因为一个不能保证稳定帧率的技术几乎无法用在实际的产品中。