2.1 CPU应用程序执行模型
几乎所有处理器都以冯·诺依曼提出的处理器结构(称为von Neumann architecture或者von Neumann model)为工作基础,冯·诺依曼被认为是计算机之父之一。在该结构中,一个具有处理单元的电子数字计算机由以下部分组成:一个用于进行二进制运算的算术逻辑单元(arithmetic logic unit,ALU),一个用来高速存储指令和数据的寄存器组(processor registers),一个用来控制指令读取的控制单元(control unit),一个用于存储所有指令和数据的内存,外加一些大容量存储设备及输入输出设备组成,如图(1)所示。

图(1):冯·诺依曼架构,图片来自Kapooht - Own work, CC BY-SA 3.0, \protect\url{https://commons.wikimedia.org/w/index.php?curid=25789639}
在冯·诺依曼模型中,处理器从内存中将指令和数据(包括地址)读取到寄存器并解码,然后执行该指令。寄存器在物理设计上靠近处理器,它是计算机所有存储设备中具有最快存取速度(通常1个CPU时钟周期)的存储设备,但是它通常只有有限的容量,例如几千字节,所以当寄存器中的指令或数据执行完毕后,就需要向主存读取数据。
在冯·诺依曼模型中,程序和数据�存储在内存中,它们和处理器是分开的,因此数据需要在内存和处理器之间进行传输,消息传递的总时间可以用一个简单的模型来描述:一个固定的开销加上一个依赖于消息长度的可变开销,即:
(式1)
这个固定开销称为延迟(latency),实际上它是指在通信介质上发送一条空消息所花费的时间,即从发送函数被调用到接收方完成接收数据的时间。延迟包括软件和网络硬件开销,消息在通信介质中��的传输时间。带宽(bandwidth)是通信介质容量的度量,表示消息的长度。
更进一步地,近年来处理器的速度得到了非常大的发展,现代处理器的运行速度通常高达4GHz;另一方面,内存的发展则主要集中在密度(即用更小的空间存储更多的数据)而不是传输速度上。所以随着处理器运行速度的提高,其花费了更多的时间用于等待从内存获取数据,不管处理器的速度多快,它都受限于内存传输速度这个瓶颈,这又称为冯·诺依曼瓶颈(The von Neumann bottleneck)。
通常有以下方法用于克服冯·诺依曼瓶颈:
- 缓存 将一些频繁使用的数据存入一个特殊的更快的存储区,当处理器需要读取这些数据时可以直接从这些存储区快速读取,而不是需要从缓慢的主存读取数据。
- 预取 将一些接下来可能会使用的数据在处理器读取之前放入到缓存区,以加速数据读取的速度。
- 多线程 使用多线程,当其中一个线程在等待数据传输的时候切换��到其他线程执行,通过使处理器保持繁忙来隐藏延迟。
缓 存
几乎所有现代处理器都设计有多个层级的缓存结构以减少从主存读取数据的时间,缓存是一种容量更小,更快的内存,缓存里的数据来自于主存。当处理器需要向主存获取指令或数据时,它首先查询缓存,如果数据不在一级缓存(L1)中,则处理器向二级或三级(L2或L3)缓存发出读取请求。如果缓存中没有此数据,则需要从主存中读取。一级缓存的工作速度通常能达到或接近处理器的时钟速度,因此,假设写入和读取都是在缓存中完成,则指令的执行很有可能接近处理器全速。一级缓存的大小通常只有16KB或32KB大小,二级缓存要慢些,但空间会大些,通常约为256KB,三级缓存要大得多,通常几兆字节大小,但是比二级缓存要慢得多。如图(2)为PS4的缓存结构。
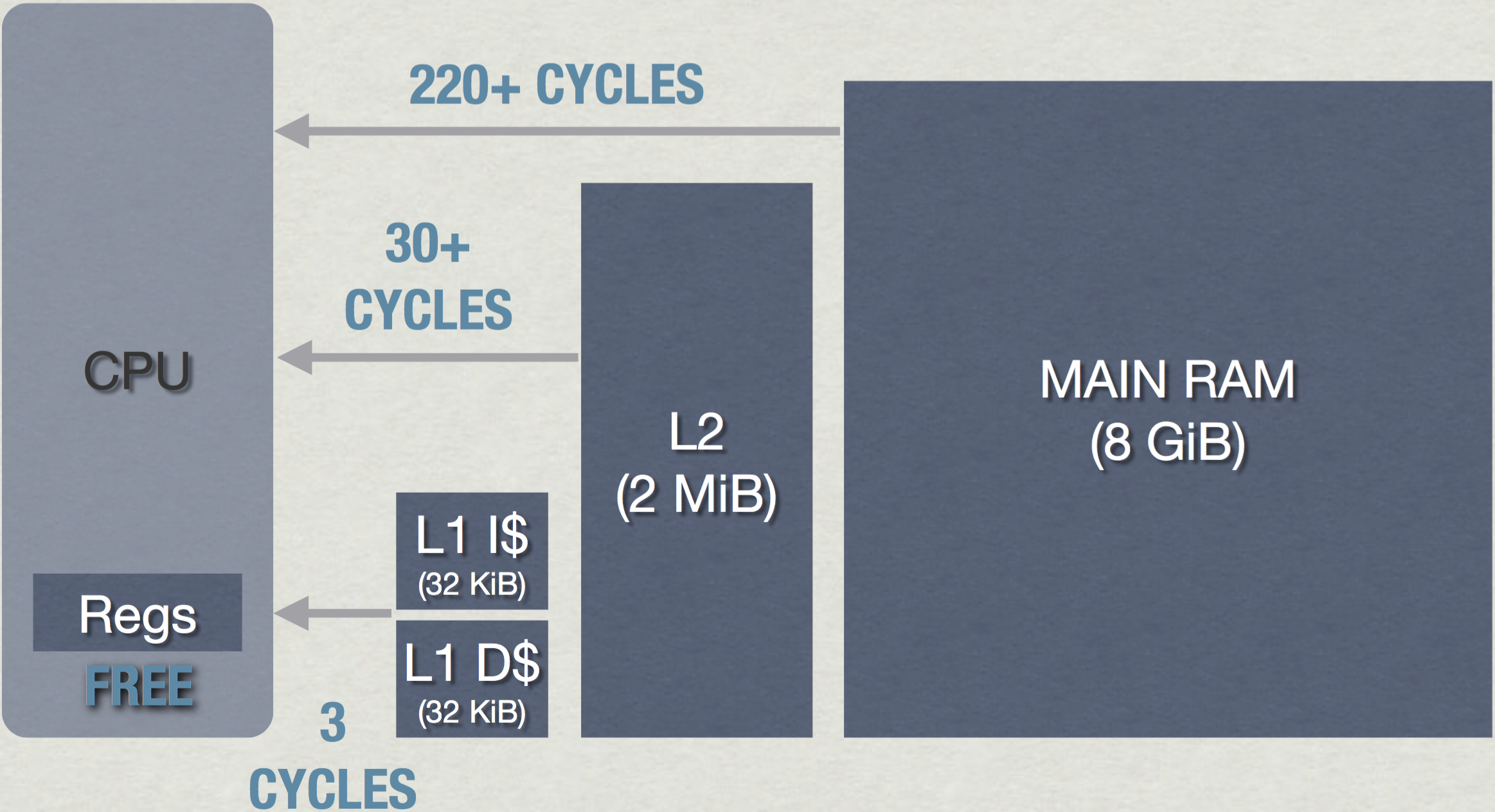
图(2):PS4分别拥有32KB的L1缓存用于存储指令和数据,L1缓存的读取速度约为3个时钟周期;2MB的L2缓存,其读取速度约为30个时钟周期;从主存读取数据则需要约220个以上的时钟周期的延迟(数据来自\cite{a:DoggedDetermination:TechnologyandProcessatNaughtyDogInc.})
现代CPU几乎都是多核的,例如PS4[cite a:PS4SystemArchitecture]有8个CPU内核。通常在缓存设计中,L1和L2级缓存都是每个核独享的,而L3级缓存是所有核共享的。在实际程序中,数据集(尤其是循环程序)可能非常大,以至于不能放在更高速的L1或L2缓存,这个时候即使设置了缓存,处理器仍然会因为受到内存吞吐率或带宽的限制,而无法发挥其所具有的处理能力。在[cite a:DoggedDetermination:TechnologyandProcessatNaughtyDogInc.]中,Jason Gregory建议要保持高性能部分的程序足够小,以使其能够存储在L2级指令缓存(L1 I$)中,同时保持高性能部分的数据足够小且相邻,使其能够存储在L1级数据缓存(L1 D$)中。
缓存的设计实际上是利用的局部性原理(locality),这包括时间局部性和空间局部性。时间局部性是指之前访问的数据很可能还要再次被访问,例如对于一个循环结构,其循环指令被多个数据使用;空间局部性是指刚刚被访问过的数据附近的数据,可能马上就会被访问,同样是循环的例子,循环的指令可能会持续访问一个数组中所有的元素。
当处理器从缓存而不是主存中取来一条指令或一个数据时,称为缓存命中(cache hit),反之称为缓存失效(cache miss)。缓存失效可能是由于处理器第一次访问一段新的指令或数据,这个时候它们还没有被读取到缓存中,这种情况的缓存失效可以通过下一节讲述的预取技术来解决。
第二种缓存失效的来源是缓存的尺寸限制,为此,我们需要理解缓存系统是如何从主存中读取数据的。主存载入到缓存的单位是一个缓存行(cache line),缓存行的大小一般是64字节,相应地,缓存系统会按照最近最少使用算法(Least recently used,LRU)替换一个旧的缓存行,这就会导致对之前缓存过的数据的访问出现缓存失效。
针对缓存系统的特点,程序员在编写程序的时候就要充分利用数据访问的局部性,例如使用顺序访问的数组。这种局部性的处理在GPU的并行计算中甚至更加重要,正如后面会讲述的关于GPU架构的内容。
缓存的设计是有代价的,例如英特尔I7-920处理器具有8MB的三级缓存,但是其占用了约左右的芯片面积。随着缓存容量的增加,用于制造处理器的硅片的物理尺寸也逐渐变大,芯片越大,制造成本越昂贵。这使人们将注意力转向另外两种延迟隐藏技术:即预取和多线程。
预 取
为了减小缓存失效的几率,预取(prefetching)技术就是通过在处理器读取数据之前预测可能会读取的数据,从而提前将其读取到缓存中,以进一步实现延迟的隐藏。
预取技术集成于处理器内部,各级缓存都有自己的预取器(prefetcher),这些预取器是一些特定的指令用来实现数据预取,一些编译器如GCC还通过在编译阶段修改源代码,在其中插入一些预取指令以实现软件预取。
L1级缓存的预取分为指令预取(L1I$)和数据预取(L1D$),对于L2和L3级缓存则是将数据和指令全部存储到一起。对于数据的预取是非常复杂的,因为程序对数据的访问往往不是线性的,所以最常用的数据预取是常数步幅(constant-stride)模式,即根据之前数据访问的模式(在一个常数范围内的步幅)预先载入当前数据邻近对应长度范围的数据,例如数据预取器能够预取以下例子中的数组A和B中的元素,因为其步幅为一个固定的常数:
for(int i = 0; i < N; i++)
A[i*4] = B[i*3];
但是数据预取器则不擅长对随机数据的预测,因此如果你的程序对数据的读取在整个内存空间随机跳跃,则预取器将变得毫无用处,例如数据预取器将不能有效处理下面的程序:
for(int i = 0; i < N; i++)
A[i*4] = B[rand()%N];
对于指令的预取,由于大部分情况下处理器按编译器编译好的顺序执行,所以程序指令数据在空间上的分布更加线性,其相对数据预取更加简单。然而仍然有一些因素使得程序指令出现非线性化,其中第一个因素是函数指针的应用,由于处理器只有在执行指令的时候才会知道其指令是追踪一个指针,所以指令预取器对函数指针没有办法进行预处理。
另一种情况是分支预测(branch prediction),即当程序中出现条件语句的时候,预取器应该怎样有效地预测分支的走向呢?和数据的随机读取一样,处理器并不知道分支的走向,这个决定只有在条件被计算出来的时候才能发生,因此其不能解决延迟的问题。所以分支预测必须记录过去的历史数据,以此计算出一定的模式并对后续的分支使用该模式来预测分支走向,这就是各种不同分支预测算法的基础。
例如对于以下条件分支语句:
if (data[c] >= 128)
sum += data[c];
\end{lstlisting}
这里data数组在0到255之间均匀分布,如果data数组按照升序的方式被排序过,则该循环的前半部分不会进入if条件语句,而后半部分会进入if条件语句。这个示例是非常容易预测的,因为分支沿着相同的方向重复很多次,使用一个简单的计数器就可以正确的预测分支走向(除了少数几次分支发生方向变化的地方):
T = branch taken
N = branch not taken
data[] = 0, 1, 2, 3, 4, ... 126, 127, 128, 129, 130, ... 250, 251, 252, ...
branch = N N N N N ... N N T T T ... T T T ...
= NNNNNNNNNNNN ... NNNNNNNTTTTTTTTT ... TTTTTTTTTT (很容易预测)
然而,如果data数组的数据是完全随机无序的,则很难对其进行分支预测,因为我们不可能预测随机数据:
data[] = 226, 185, 125, 158, 198, 144, 217, 79, 202, 118, 14, 150, 177, 182, 133, ...
branch = T, T, N, T, T, T, T, N, T, N, N, T, T, T, N ...
= TTNTTTTNTNNTTTN ... (完全随机 - 很难预测)
所以对于分支条件语句,在编写程序的时候应该尽量考虑其指令的连续性,这些对处理器特性的运用会大大减少延迟,使处理器能够更有效地工作。尤其对于像光线追踪这种每帧数亿的光线计算,充分的对程序结构及数据进行优化会带来巨大的性能提升,我们将在后面的章节看到对这些知识的运用。