4.3 对分布$p(x)$进行采样

由上节的内容可知，蒙特卡洛方法涉及两个基本的步骤：采样和求平均值，本节就讨论几种不同采样方法。

首先我们定义什么是采样，考虑一个定义域空间$\Omega_0$以及一个概率密度函数$p(x)$，其中$x\in\Omega_0$，满足：

$${\rm \int}_{\Omega_0}p(x){\rm d}x=1$$

（式1）

采样的过程是这样一个算法，它能够从$p(x)$对应的随机变量$X$中产生一系列随机数$X_1,X_2,...$，使对于任意$\Omega\in\Omega_0$满足：

$$P\{X_k\in\Omega\}={\rm \int}_{\Omega}p(x){\rm d}x\leq 1$$

（式2）

实际上我们不能直接从$p(x)$产生随机数，在计算机程序中这个过程必须要求首先具有某些基础随机数的一个序列。我们可以借助计算机操作系统提供的${\rm random}(u)$函数来产生一个均匀分布的随机数，又称为伪随机数（pseudorandom numbers）, 定义这些随机数的值为$\xi_1,\xi_2,\cdots$，它们可以用来作为采样所需的基础随机数。

逆变换算法

逆变换算法是1947年由乌拉姆提出的，它的定义如下：设$X$是连续随机变量，其累计分布函数为$P_X$，如果随机变量$Y$是一个$[0,1]$上的均匀分布，则随机变量$P^{-1}_X(Y)$具有和$X$一样的概率分布。

逆变换算法的直观解释可以由图（1）得出，图中$dy$表示的随机变量是[0,1]上的均匀分布，由式[ref eq:mc-continuous-pdf]可知，随机变量$X$中的值落于${\rm d}x$区间的概率$p(x)= \cfrac{{\rm d}P(x)}{{\rm d}x}= \cfrac{{\rm d}y}{{\rm d}x}$，所以$Y$上的均匀分布被映射到满足$p(x)$的随机变量$X$上。

图（1）：逆变换算法将一个满足[0,1]上的均匀分布的随机变量$Y$，通过$X=P^{-1}(Y)$映射到满足概率分布$p(x)$的随机变量$X$上

以下我们以一个离散分布的例子来进一步解释逆向变换算法的过程，设一个离散随机变量具有4个可能的值，其对应的概率分别为：$p_1,p_2,p_3$和$p_4$ ，这些概率满足：$\sum_{i=1}^{4}p_i=1$, 该随机变量对应的概率密度函数如图（2）所示。

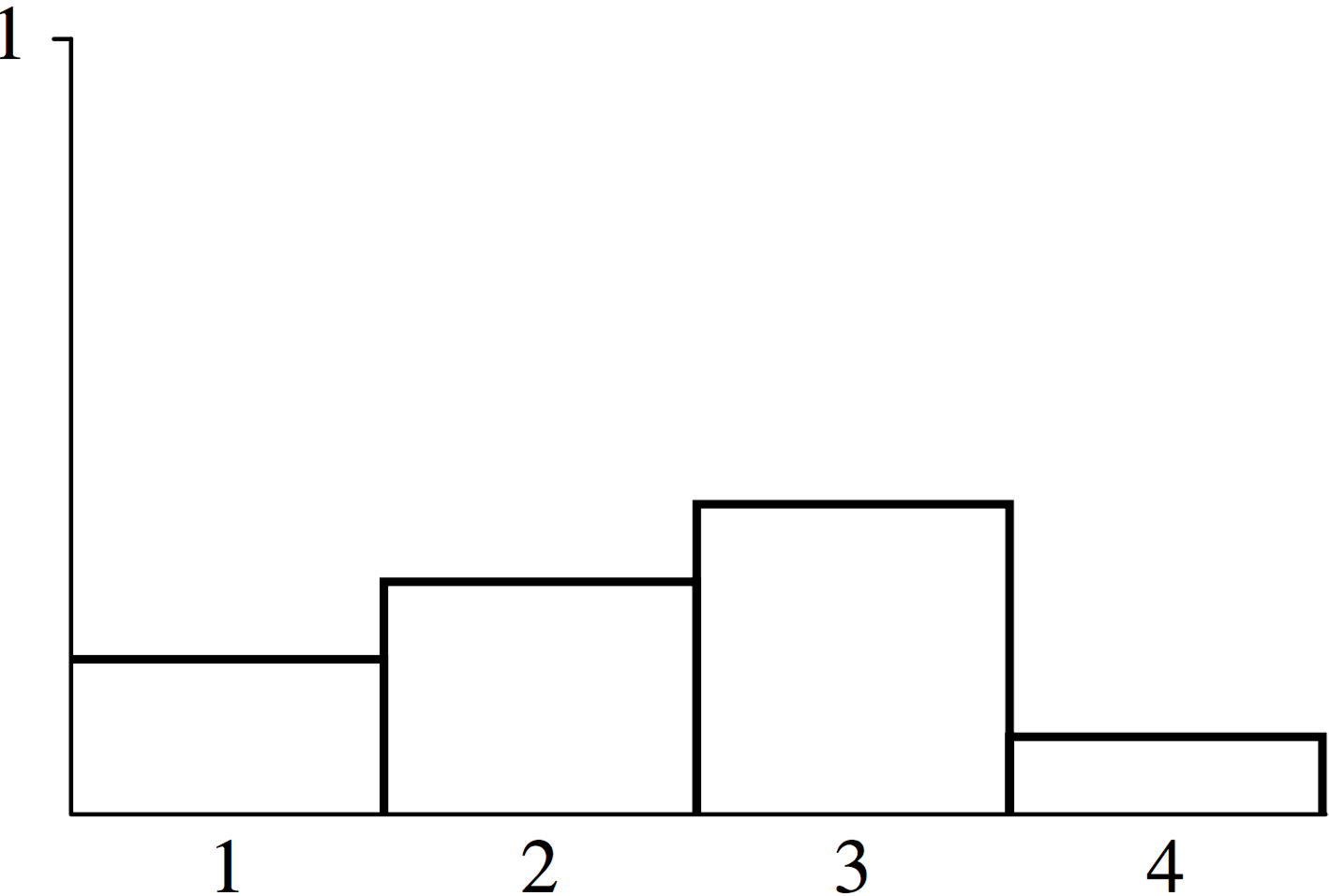
图（2）：一个具有4个输入事件的离散随机变量的概率密度分布，每个随机数$x_i$的概率为$p_i$

为了使用逆变换算法从一个任意分布中进行采样，首先需要求出其对应的累积分布函数 $P(x)$，对于连续随机变量，$P$是$p$在全定义域上的积分，对于离散随机变量，可以使用前$i$个$p$的值的和作为$P(x_i)$的值，如图（3）所示。注意，为了满足所有随机事件的概率之和为1，最右边的条的高度应该为1。

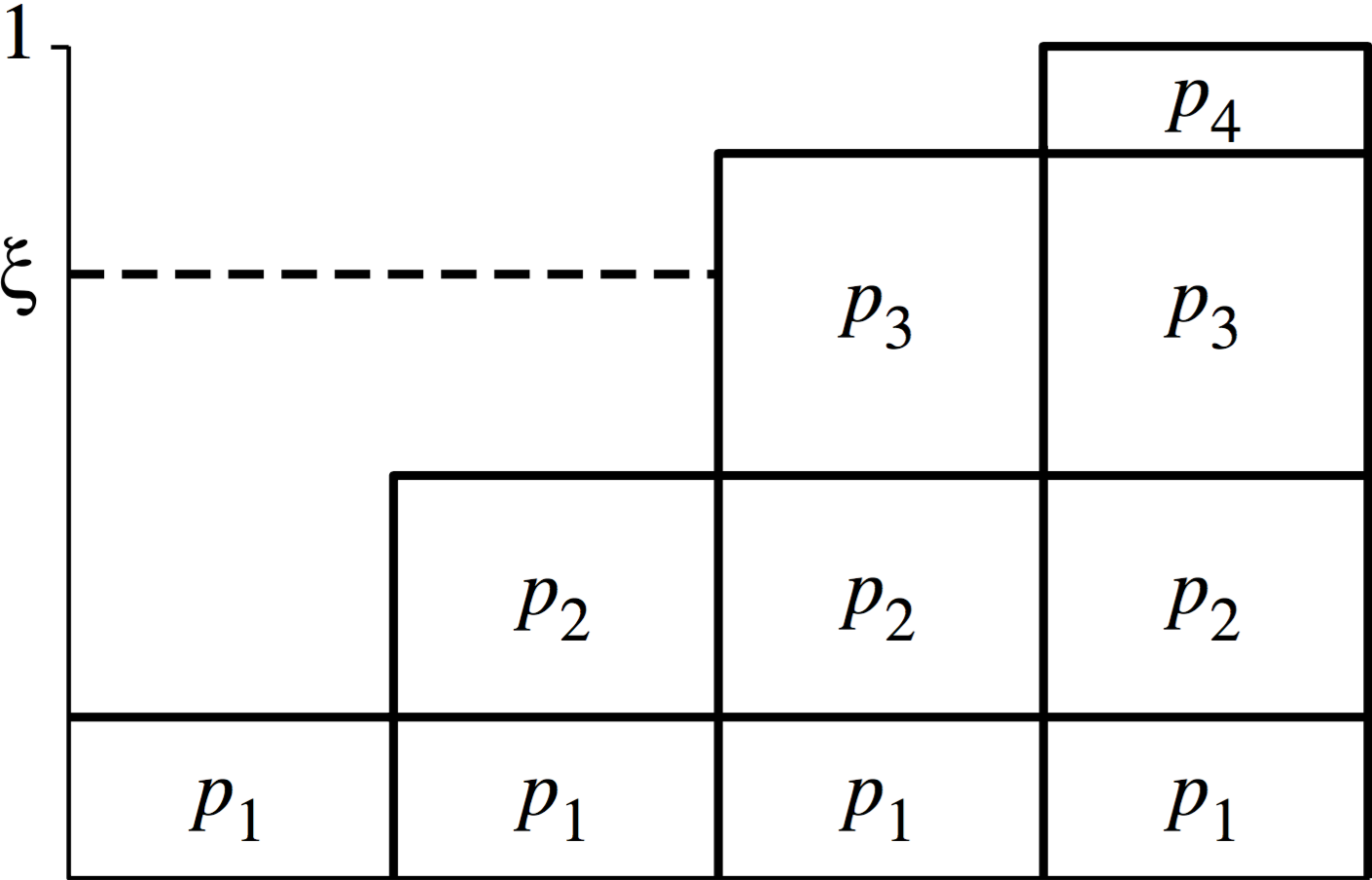
图（3）：从离散随机变量的概率密度函数$p$构建概率分布函数$P$的过程，$[0,1]$上均匀分布的随机数$\xi$被按照概率分布映射到离散随机变量$X$上

在图（3）中，一个标准的$[0,1]$上的均匀分布的随机变量分布在纵坐标上，通过在水平方向上延伸$\xi$可以和具有概率$p_i$的第$i$个输入事件相交，因为$\xi$是服从均匀分布的，所以具有更大概率的$p_3$比$p_4$拥有更多的机会被选择，所以通过这样的方式，$[0,1]$上的均匀分布$\xi$被完全变换为服从概率密度函数$p(x)$的离散随机变量$X$。

通过上述的示例，我们可以推导出使用逆变换算法从一个概率密度函数$p(x)$产生随机数$X_i$的步骤：

1. 首先计算$p(x)$的累计分布函数：$P(x)={\rm \int}_{0}^{x}p(x^{'}){\rm d}x^{'}$。
2. 其次计算累计分布函数的反函数：$P^{-1}(x)$。
3. 然后从一个$[0,1]$上的均匀分布产生一个随机数$\xi$。
4. 最后将随机数$\xi$代入$P(x)$的反函数求出满足$p(x)$分布的随机数：$X_i=P^{-1}(\xi)$。

取舍算法

在许多情况下，逆变换算法无法被使用：首先是某些累积分布函数无显式解析表达式，因此写不出反函数，例如某些概率密度函数没有边界，不能归一化；其次是反函数无显式表达式，因此解不出反函数；再次是在整个求累积分布函数和反函数的过程中，这里面可能涉及大量初等函数的计算，因此采样成本很高。

为了在计算机中对任意分布函数进行采样，冯·诺伊曼于1947年提出了取舍算法（acceptance-rejection method），这种方法不需要对概率分布函数执行归一化，并且它通常只需要直接使用计算机系统提供的均匀分布的随机数$\xi$即可。

取舍算法的思路很简单，它和本章开头讲述的蒲丰投针（如图[ref f:mc-pi]所示）实验的原理类似，考虑一个任意函数$f(x)$（注意，这里的$f(x)$实际上是一个分布函数，然后在取舍算法中它通常并不是归一化的，因此我们偏向于称其为更具广泛意义的函数$f(x)$而不是归一化的$p(x)$。）被限定在$[a,b]$区间，在此区间外的所有值均为0，如图（4）所示。

图（4）：取舍算法在一个能够完全包围住$f(x)$的空间上均匀采样，然后选择（接受）处于函数$f(x)$范围内的采样值用来作为采样值，其他值则被抛弃（拒绝）

在这种情况下产生一个随机变量$Y\sim f(x)$的过程非常直观，它可以被描述为以下接受-拒绝的过程：

1. 产生一个$[a,b]$上均匀分布的随机数：$X\sim U(a,b)$。
2. 产生一个$[0,c]$上独立于$X$的均匀分布的随机数：$Y\sim U(0,c)$($c$是函数$f(x)$的最大值)。
3. 如果$Y\leq f(X)$，则接受，接受的随机数为$Z=X$，否则$X$被拒绝，算法返回到第一步重新产生新的随机数。

需要注意的是，每次采样产生的随机数矢量$(X,Y)$实际上是均匀地分布于一个矩形区域$[a,b]\times [0,c]$，因此被接受的随机数矢量$(X,Y)$则会均匀分布于函数$f(x)$以下的区域，这意味着被接受的随机数$X$服从概率分布$f(x)$。

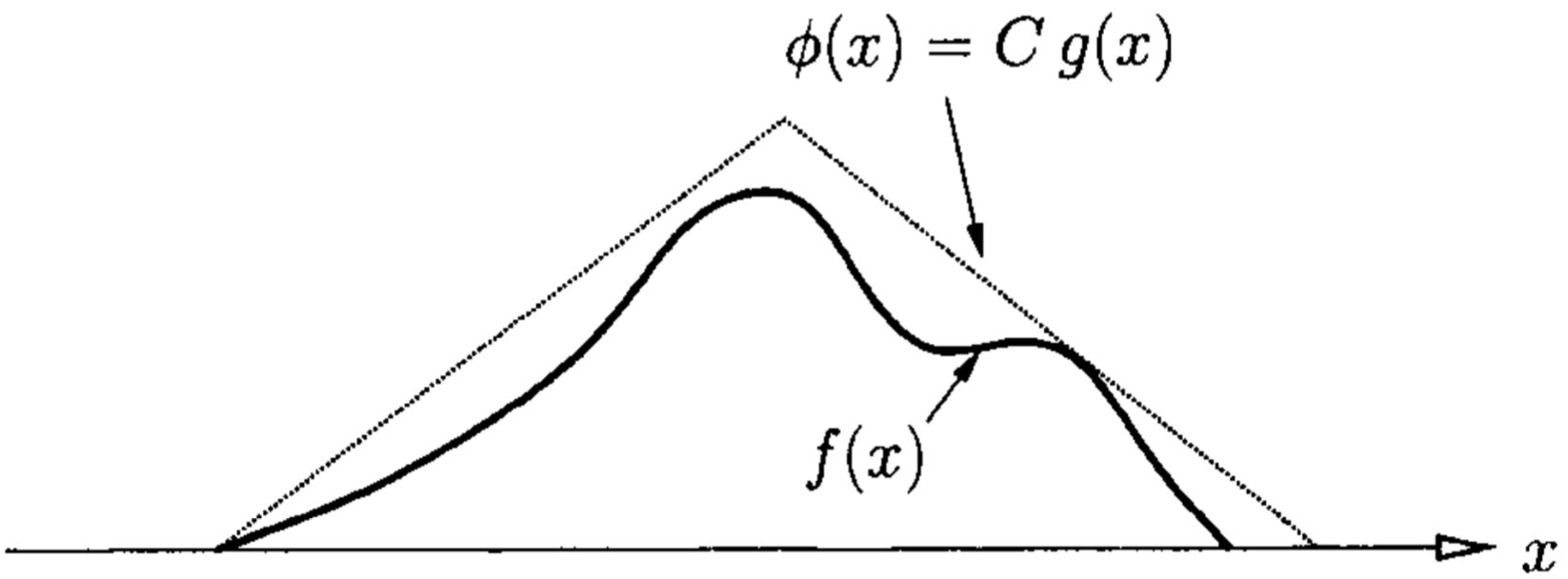
图（5）：为了减少被拒绝的采样值的数量，使用一个接近$f(x)$而不是$c$的函数$\phi$来包围$f(x)$

取舍算法的缺点是其效率比较低，因为在接受一个随机数之前，大量的随机数被拒绝了。为了减少被拒绝的随机数的数量，实践上通常使用一个建议分布（proposal distribution）$\phi (x)=Cg(x)$来逼近$f(x)$（称为目标分布）的分布，其中$g(x)$是一个简单的函数，它通常能够比较容易的（例如使用逆向变换算法）产生随机数常数$C$用来保证$\phi (x)$能够完全覆盖$f(x)$，即：$\phi (x)\geq f(x)$，如图（5）所示。所以上述的取舍算法可以写为：

1. 产生随机数：$X\sim g(x)$。
2. 产生随机数：$Y\sim U(0,Cg(X))$。
3. 如果$Y\leq f(X)$, 则接受随机数：$Z=X$，否则返回第一步。

取舍方法不需要对函数执行归一化，只需要找到一个能够覆盖该分布函数的更简单的分布（建议分布）即可，例如对于：

$$f(x)= \cfrac{2}{\pi(1-x^2)^{ \frac{1}{2}}},0<x<1$$

（式3）

可以使用更简单的建议分布函数：

$$g(z)= \cfrac{1}{2(1-z)^{ \frac{1}{2}}}$$

（式4）

注意，虽然对于一维的函数，取舍算法需要产生两个随机数来做取舍判断，但是由于它减少单次采样的计算成本，因此它和逆向变换算法仍然具有可比性。

随机变量的变换

在前面讨论逆向变换算法的时候，我们介绍了一种技术，它可以将一个满足均分分布的随机变量转换为一个满足任意分布的随机变量。本节，我们将讨论与之相关的一个更一般的问题：即将满足任意分布的一个随机变量转换为满足另一个分布的随机变量。

假设随机变量$X$的累积分布函数为$F_X(x)$，以及概率分布函数为$f_X(x)= \cfrac{{\rm d}F_X}{{\rm d}x}$，另一个随机变量$Y=y(X)$是关于$x$的连续单调递增函数，如图 （6）(a)所示，我们的目标是求出$Y$的累积分布函数$F_Y(y)$的形式。

图（6）：$y$是一个连续函数，其中(a)是关于$x$的单调递增函数，(b)是关于$x$的单调递减函数

由于$Y$是单调递增的，因此有：

$$y(X)\leq y(x), \text{ if } X\leq x$$

（式5）

所以$Y$的概率为：

$$P\{y(X)=Y\leq y(x)\}=P\{X\leq x\}$$

（式6）

或者写成：

$$F_Y(y)=F_X(x)$$

（式7）

$X$和$Y$的概率分布函数之间的关系，可以通过对式（7）两边求微分得出：

$$f_Y(y) \cfrac{{\rm d}y}{{\rm d}x}=f_X(x)$$

（式8）

现在假设$y(X)$是关于$X$的单调递减函数，如图（6）(b)所示，根据上面类似的推导过程，得到：

$$f_Y(y) \cfrac{dy}{dx}=-f_X(x)$$

（式9）

所以随机变量$X$和$Y$之间概率分布函数之间的关系为（通过组合式（8）和式（9））：

$$f_Y(y)=| \cfrac{dy}{dx}|^{-1}f_X(x)$$

（式10）

上式反映出这样一个事实，即$X$在${\rm d}x$区间的所有值被映射到$Y$在${\rm d}y$区间内，如图（7）所示。

图（7）：$X$在$dx$区间的所有值被映射到$Y$在$dy$区间内