4.5 方差缩减

通过前面的内容，我们已经熟悉了使用蒙特卡洛方法求积分的基本方法，这里再总结一遍，它基本上可以分为三个步骤：首先，使用前面讲述的一些采样方法（如逆向变换算法）从一个目标概率分布中采样产生一系列随机数$x_i$；接着，将每个随机数代入式$\cfrac{f(x_i)}{p(x_i)}$中求得每个样本的统计值；最后，求出这些统计值的平均值用来近似（估计）函数$f(x)$的积分。

由于蒙特卡洛方法是一个统计过程，因此方差始终存在，设计更有效的估计是蒙特卡洛方法研究中的主要领域，从蒙特卡洛方法诞生至今已出现非常多的方差缩减（variance reduction）的方法，但是由于蒙特卡洛方法在图形学中的运用往往都是要求计算不要太复杂，所以本节仅介绍少数几种计算机图形学中常用的方差缩减方法。

重要性采样

重要性采样（importance sampling）是蒙特卡洛方法中最基础也是非常重要和有效的方差缩减方法，它通过选择对一个与目标概率分布具有相似形状的分布函数进行采样来减少方差。直观上看，重要性采样试图在被积函数中贡献更高的区域放置更多的采样点，以体现这部分区域的重要性。

给定一个概率分布$p(x)$，以及从该分布采样得到的$N$个随机数$x_i$，根据蒙特卡洛方法，被积函数$f(x)$的积分$I$可以通过以下式来进行估计：

$$I_N= \cfrac{1}{N}\sum_{i=1}^{N} \cfrac{f(x_i)}{p(x_i)}$$

（式1）

一个完美估计（perfect estimator）的方差应该为0，由此，相对理想的采样概率密度函数$p(x)$可以从下式推导出：

$$0=\sigma^2= \cfrac{1}{N}{\rm \int}( \cfrac{f(x)}{p(x)}-I)^2p(x){\rm d}x$$

（式2）

因为$p(x)$是非零的，所以：

$$p(x)= \cfrac{|f(x)|}{I}$$

（式3）

如果我们使用这样的概率密度函数进行采样，其方差会被完美地消除，然而，这个理想的$p(x)$要求我们首先计算出$I$的值，而这正是我们试图去求解的，因此找到这样理想的$p(x)$是完全不可能的。

不过，我们可以选择和被积函数$f(x)$具有相似形状的概率密度函数来减少方差，直观上理解，它使得每个样本值$\cfrac{f(x_i)}{p(x_i)}$趋近于一个常数，也即是通过减少每个$\cfrac{f(x_i)}{p(x_i)}$值的变化范围来减少方差，因为常数的方差为0。

图（1）：重要性采样（右图）通过选择和被积函数具有相似形状的概率密度函数来进行采样，以减小统计方法导致的方差；此外，任意选择的分布（左图）可能比均匀分布（中图）具有更大的方差

图（1）展示了选择不同的概率密度函数$p(x)$对被积函数$f(x)$估计的差异，右边小图的重要性采样会比左图任意分布采样以及中间小图的均匀采样拥有更小的方差，此图也说明任意选择的采样（左边小图）可能比使用均匀分布（中间小图）的方差要大很多。所以从这里可以看出选择用于产生采样的概率密度函数的重要性，尽管蒙特卡洛方法本身没有限制对概率密度函数的选择，但是选择不好的概率密度函数会大大增加蒙特卡洛估计的方差。

复合重要性采样

在实际的情景中，计算机图形学中的被积函数通常是具有非常复杂，不正常的分布的，它们可能是不连续的，通常在少数区域拥有奇点（singularities）或者一些较大的值，所以很难找到一个简单的与其被积函数相似的分布用来进行重要性采样。

例如，考虑渲染中最普通的直接光源的计算，其公式如下：

$$L_o({p},\mathbf{v})={\rm \int}_{\Omega}f_r(\mathbf{l},\mathbf{v})\otimes L_i({p},\mathbf{l})\cos\theta_i {\rm d}\omega_i$$

（式4）

我们可能选择$L_i$或$f_r$来进行重要性采样，但是这两者都会产生糟糕的结果，因为一个不好的分布比均匀分布的方差要更大。考虑一个接近镜面的BRDF的表面被一个面积光照射的例子，如图（2）所示，这里面积光源的分布$L_i$被用来作为采样函数，因为BRDF是几乎镜面的，所以除了沿镜面反射光方向$\omega_i$，大部分光源上的采样对最终光照的贡献几乎为0，因此估计的方差会非常大；虽然这种情况下使用BRDF分布作为采样分布比较合适，但是对于被很小面积光源照射的漫反射或高光表面，使用BRDF作为采样分布仍然会导致很大的方差，此时我们应该尽可能地在光源上产生更多地采样点。

因此，我们通常需要使用更复杂的采样方式（而不是简单地从一个简单分布采样）以使估计具有更低的方差，这通常涉及根据被积函数的分布特征对其进行区域划分，然后在不同特征的区域上使用不同的分布函数进行采样，最后再将这些结果以某种方式进行混合。

图（2）：对于一个被面积光照射的高光表面的直接光进行采样，这里有4个圆形面积光源，它们分别拥有不同的辐射照度及颜色，在四个圆形光源上面是一个聚光灯光源，所有的光源具有相同的辐射能量；下面是4个拥有不同粗糙度的高光矩形塑料（图片来自\cite{a:OptimallyCombiningSamplingTechniquesforMonteCarloRendering}）

复合重要性采样（multiple importance sampling，MIS）就是这样一类采样方法，它非常简单而有效，它提供一个策略使得可以从多个不同的分布中采样，然后对这些不同的采样结果进行加权组合。根据原始论文[cite a:OptimallyCombiningSamplingTechniquesforMonteCarloRendering]，复合重要性采样可以简单地分为以下几步：

• 首先，选择一系列的重要性分布$p_1,...,p_n$，使得对于被积函数$f$的每一个潜在值比较大的区域$\Omega_i$，在那个区域它能够被其中的一个单个重要性分布$p_i$近似（形状相似），如图（3）所示。通常一个复杂的被积函数是多个不相关的简单分布的乘积的形式，所以这些重要性分布的最佳来源就是这些简单分布，使得$p_i$可以正比于每个简单分布。
• 然后，从每个分布$p_i$产生$n_i$个随机数$X_{i,1},\cdots,X_{i,n_i}$，这通常是根据某种策略基于$f$和$p_i$提前（在采样之前）计算而出。
• 最后，对每个分布的结果使用一个组合估计（combined estimator）进行加权组合以对积分进行估计。

复合重要性采样中的组合估计表达式如下：

$$I_N=\sum_{i=1}^{n} \cfrac{1}{n_i}\sum_{j=1}^{n_i}\omega_i(X_{x,j}) \cfrac{f(X_{i,j})}{p_i(X_{i,j})}$$

（式5）

上式说明复合重要性采样是多个重要性采样的一个加权组合，它将整个空间按一定的形式划分，然后对每个划分的区域使用不同的采样技术，所以$\sum^{n}_{i=1}$表示的就是这些不同采样技术的和；$\sum^{n_i}_{j=1}$表示一种特定的采样技术$p_i$的估计值，但是由于在每个$f(x){\rm d}x$区间内，每种技术只贡献其中一部分值，所以每种技术的估计结果被乘以一个系数$\omega_i(X_{i,j})$，$\omega_i(x)$可以在每个$x$处的值不一样，只要保证对于每个$x$位置处满足$\sum^{n}_{i=1}\omega_i(x)=1$就行，这样就能保证每个$x$处的值被正确估计。

图（3）：复合重要性采样对多个采样技术进行组合，即加权和，并可以根据每个区域内多个采样技术的贡献度来调整混合权重，使得联合估计结果能够充分发挥每个采样技术的优势

我们可以再解释一下这个加权系数$\omega_i(x)$的由来及原理，假设现有两个采样技术$p_1(x)$和$p_2(x)$如图（3）所示，两种采样技术单独的采样结果分别为$\cfrac{1}{n_1}\sum \cfrac{f(x)}{p_1(x)}$和$\cfrac{1}{n_2}\sum \cfrac{f(x)}{p_2(x)}$，它们都分别能够完全估计目标积分$I$，但是各自的方差都很大。所以我们使用将两种采样技术进行组合，所以每个采样的区域是两个采样技术的加权和，为了尽可能发挥每个采样技术的优势，我们往往尽可能保证在每个区域贡献更高的采样技术拥有更高的权重，这也正是后面平衡启发式的原理。

我们可以证明复合重要性采样的联合估计是无偏的：

$$E[I_N]=\sum_{i=1}^{n} \cfrac{1}{n_i}n_i{\rm \int}_{\Omega} \cfrac{\omega_i(x)f(x)}{p_i(x)}p_i(x){\rm d}\mu (x)={\rm \int}_{\Omega}f(x){\rm d}\mu (x)$$

（式6）

基于以上联合估计，我们可以选择使用不同的权重系数$\omega_i(x)$来混合多个采样分布，以尽可能减少估计的方差。

平衡启发式

考虑如下的权重系数函数：

$$\hat{\omega}_i(x)= \cfrac{c_ip_i(x)}{\sum_j c_jp_j(x)}$$

（式7）

这里$c_i$是每个采样分布$p_i$对应的采样数量的比例，$c_i= \cfrac{n_i}{N}$，所以$\sum_i c_i=1$，$c_i$是一个固定的数值，它在采样之前确定。这个权重系数函数$\hat{\omega}_i(x)$拥有一个属性，那就是采样值$\cfrac{\hat{\omega}_i(x)f(x)}{n_ip_i(x)}$完全与$i$无关，因为每个$x$的采样值对于所有采样技术都是无关的，所以我们称这种策略为平衡启发式（balance heuristic）。

代入$\hat{\omega}_i$到式（5），我们得到标准的蒙特卡洛估计：

$$I_N= \cfrac{1}{N}\sum_{i=1}^{n}\sum_{j=1}^{n_i} \cfrac{f(X_{i,j})}{\overline{p}(X_{i,j})}$$

（式8）

这里：

$$\overline{p}(x)=\sum_{i=1}^{n}c_ip_i(x)$$

（式9）

$\overline{p}(x)$又称为联合采样分布（combined sample distribution），对于总数$N$个采样，其中每个$n_i=c_i N$个独立的随机数$X_{i,j}$分别从分布$p_i$采样而得。

这就是平衡启发式的核心思想，也是一种很自然的组合多种采样技术的方式。我们使用一个单一的与$i$完全无关的分布$\overline{p}(x)$来表述这种组合方式。更进一步理解，$\overline{p}(x)$是一个由每个$X_{i,j}$组成的随机变量$X$的分布，每个随机数的概率为$1/N$。

除了平衡启发式，还存在一些其他的不同形式的混合系数函数，感兴趣的读者可以参考 [cite a:Safeandeffectiveimportancesampling,a:AdaptiveMultipleImportanceSampling,a:ANADAPTIVEPOPULATIONIMPORTANCESAMPLER,a:EfficientMultipleImportanceSamplingEstimators]等。

分层采样

重要性采样技术在被积函数更重要的区域放置更多的随机数来更好地逼近原始分布，然而它并不能消除由于随机数导致的丛聚（clumping），由于概率密度函数产生的随机数仅仅指示的是一个期望值，而不是一个绝对的数量。这些丛聚现象会导致估计的方差增大，因为它可能导致其他某些区域可能被忽略了。

与重要性采样调整采样函数$p(x)$的思路不同，针对上述问题，另一类常见的方差缩减的技术基于小心地设置采样随机数在被积函数区域的放置，其目标是使它们能够捕捉到被积函数的各部分重要信息（不至于由于随机数的丛聚导致某些部分被忽略），这类方法的结果是随机数不再是完全随机的，这类方法通常用作重要性采样等技术的一种补充。本节我们讨论分层采样技术，而下一节讨论完全非随机的拟蒙特卡洛方法。

分层采样（stratified sampling）将被积函数的定义域$\Omega$划分成多个彼此不相交的子定义域$\Omega_1,...,\Omega_n$，即满足：

$$\bigcup_{i=1}^{n}\Omega_i=\Omega$$

（式10）

每个子定义域$\Omega_i$称为一个阶层（stratum），在每个阶层$\Omega_i$内，固定数量的$n_i$个随机数分别从采样分布$p_i$采样而得。在每个阶层内，其蒙特卡洛估计为：

$$F_i= \cfrac{1}{n_i}\sum_{j=1}^{n_i} \cfrac{f(X_{i,j})}{p_i(X_{i,j})}$$

（式11）

这里，$X_{i,j}$是从采样分布$p_i$中采样产生的第$j$个随机数，因此整个被积函数的估计为：

$$F=\sum_{i=1}^{n}v_iF_i$$

（式12）

这里$v_i$表示每个阶层$i$ ($v_i\in(0,1]$)占整个定义域空间的体积的比例，该估计的方差为：

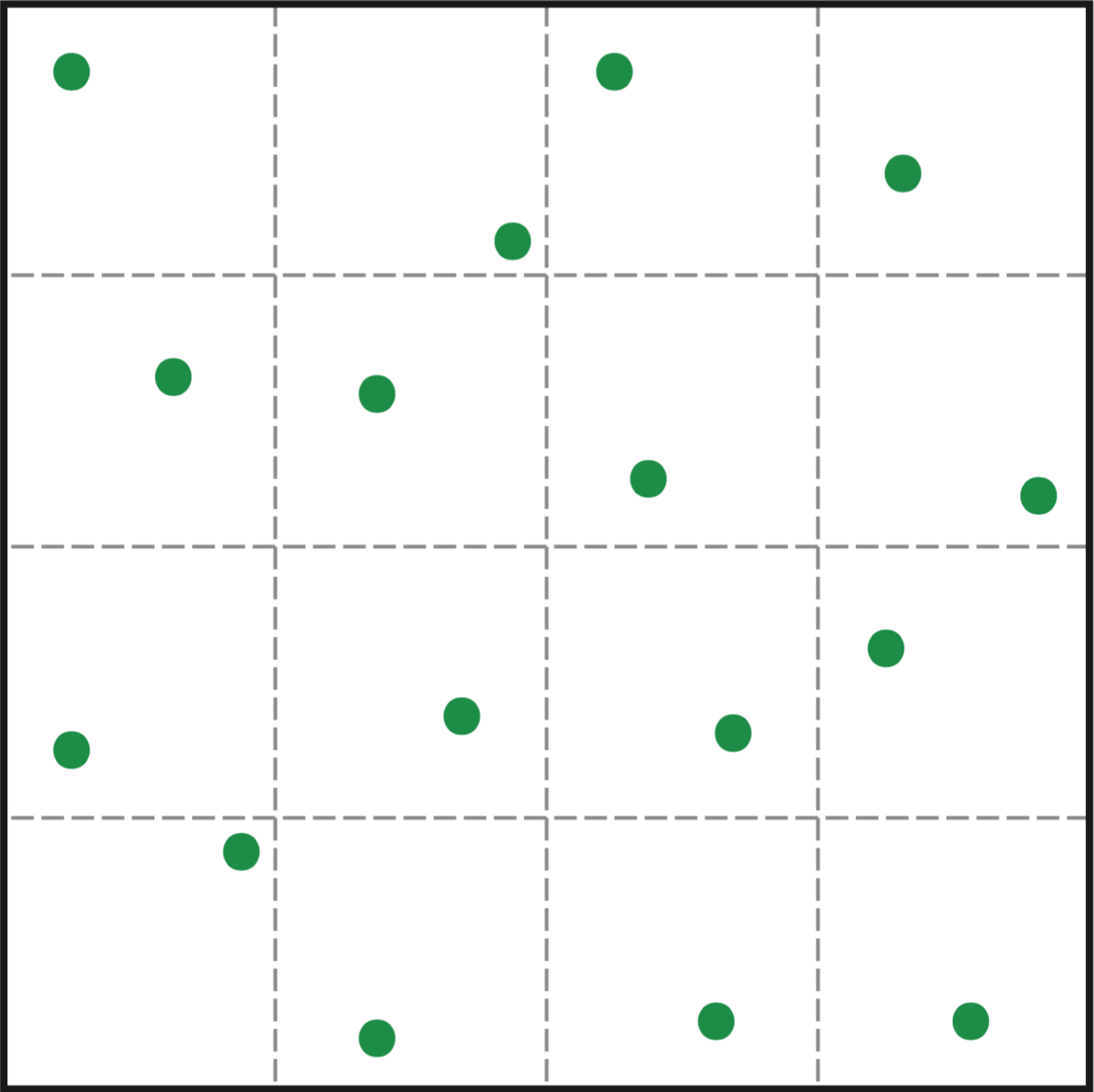
图（4）：16个随机采样值和分层采样的比较，完全随机的采样(a)可能会导致丛聚，丛聚可能使得被积函数其他区域采样不足从而增加估计的方差

$$V[F]=\sum_{i=1}^{n} \cfrac{v_{i}^2 \sigma_{i}^2}{n_i}$$

（式13）

这里$\sigma_{i}^2=V[f(X_{i,j})]$表示在阶层$\Omega_i$内的估计的方差。

为了与其他非分层采样方法进行比较，假设$n_i=v_iN$，$N$为估计全部使用的样本，上式可以简化为：

$$V[F]= \cfrac{1}{N}\sum_{i=1}^{n}v_{i} \sigma_{i}^2$$

（式14）

另一方面，非分层采样估计的方差可以表示为（感兴趣的读者可以参见[cite a:RobustMonteCarloMethodsforLightTransportSimulation]第51页的推导过程）：

$$V[F]= \cfrac{1}{N}\Bigg[ \sum_{i=1}^{n}v_{i} \sigma_{i}^2 +\sum_{i=1}^{n}v_i(\mu_i-I)^2 \Bigg]$$

（式15）

其中，$\mu_i$表示阶层内$f$的平均值（或者说期望），$I$表示整个定义域内$f$的期望，因为右边的和总是非负的，所以分层采样永远不会增加估计的方差，如图（4）所示。

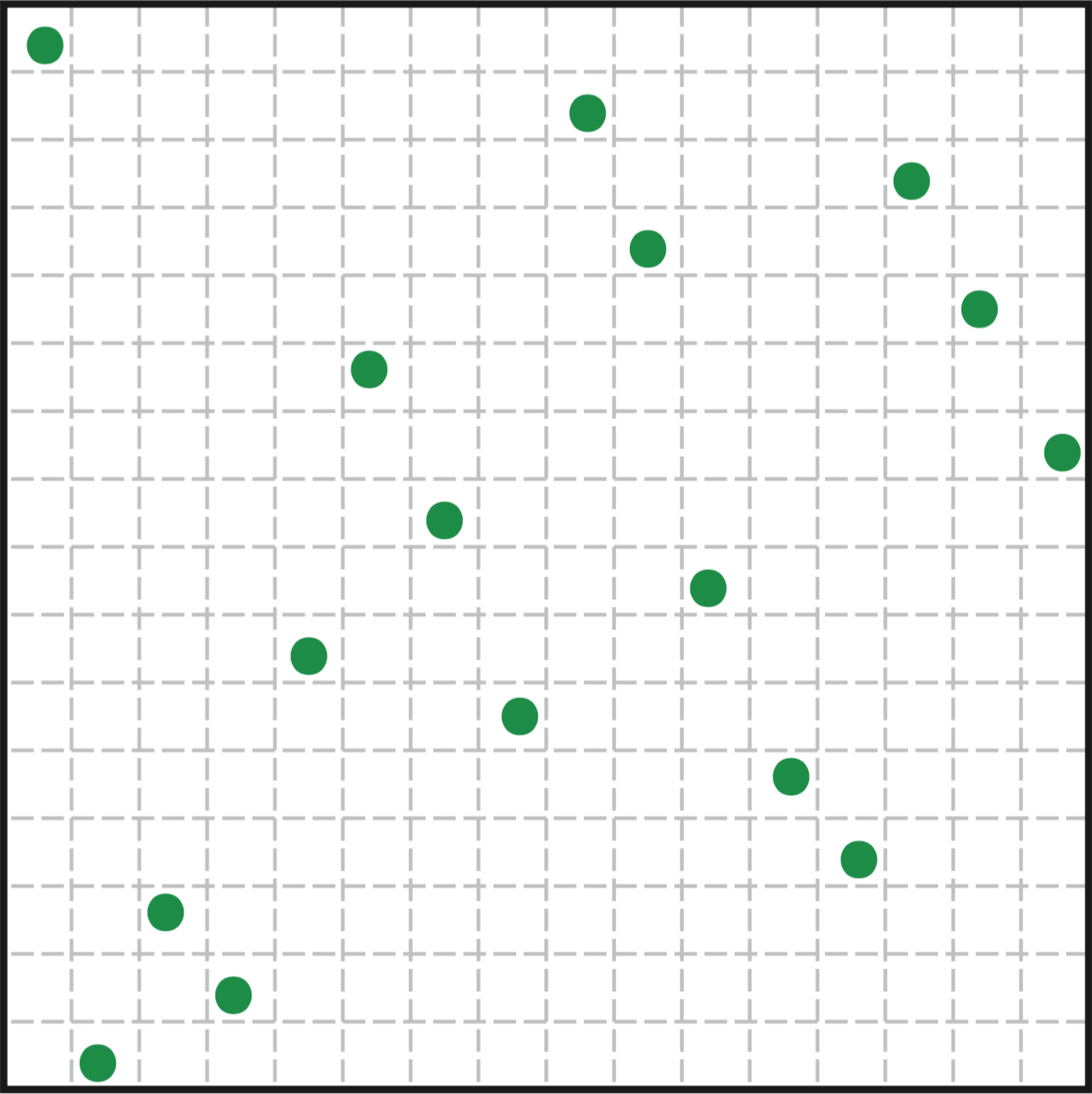
图（5）：在2维的空间中，$N$-rooks算法保证每个行或列不会放置超过两个随机数

分层采样方法的主要缺点是对高维积分是无效的，一般地说，$d$维的定义域空间可能需要$N^d$个阶层划分，针对这个问题，一些变体采样方法被提出，例如$N$-rooks算法保持总的采样数量是固定的，即其与定义域的维度无关。例如，考虑一个2维的函数，使用每个阶层一个采样点的分层采样，一共需要$N^2$个阶层划分；$N$-rooks算法则将这$N$个采样点均匀地分配在各个阶层空间，在这个例子中就是保证每个行和列的组合只包含一个采样点，如图（5）所示，关于$N$-rooks算法，更详细的描述参见Shirley的博士论文[cite a:PhysicallyBasedLightingCalculationsForComputerGraphics]。

沿着这种改变随机性的思路，拟蒙特卡洛方法则完全去掉随机性，使得随机数完全按照某种固定序列均匀分布来避免丛聚，我们将在下一节讨论拟蒙特卡洛方法。

拟蒙特卡洛方法

虽然大数定律证明，当采样数量趋近于无穷的时候，蒙特卡洛估计趋近于期望值的概率为1，但是传统蒙特卡洛方法的收敛速度非常慢，其标准差$\sigma\propto \cfrac{1}{\sqrt{N}}$，即增加4倍的采样数量才能换来2倍的精确度提升。

在上一节中已经证明，分层采样减少了蒙特卡洛估计的方差，这主要是由于阶层的划分减少了随机数导致的丛聚，那么更进一步，我们可不可以采用完全均匀的采样来代替随机分布，使得蒙特卡洛估计的方差进一步降低，收敛速度更快呢？

重新思考蒙特卡洛方法，其随机变量的独立性是指其对应的随机事件之间是不相关的，但是蒙特卡洛方法并没有限制随机数产生的方式，它只要求采样的随机数满足对应的分布。传统的采样方式是使用电脑的伪随机数来进行的，这种随机的特征导致每个随机数并不知道其他随机数的任何信息，所以其分布可能出现丛聚，减慢了收敛速度。所以，理论上如果我们使用确定性（非随机）的方法来产生均匀地分布，那么蒙特卡洛方法的模拟过程不会受到影响，并且收敛速度可以加快。

拟蒙特卡洛方法（Quasi-Monte Carlo method）就是这样一种方法，它和传统蒙特卡洛方法的唯一不同仅在于随机数产生的方式，拟蒙特卡洛方法使用低差异（low-discrepancy）序列，这些序列是通过数论方法产生的高度均匀的拟随机数序列，例如霍尔顿序列，索波尔序列等。本节我们将首先讨论均匀性以及拟蒙特卡洛方法的方差，然后介绍几种常见的低差异序列。

设$a$和$c$是$[0,1)^d$区间内的点，对于$a,c$的每个分量$i$都满足$a_i<c_i$，则$[a,c)$可以表示一些点$x$组成的一个盒子区域，对于每个分量$i$这些点满足$a_i\leq x\leq c_i$，我们用$|[a,c)|$表示这个d-维盒子的体积。

设$x_i$是$[0,1)^d$上的随机数，为了分析一个序列的均匀性（uniformity）对收敛速度的影响，我们需要一个数值方法来度量一个序列有多么均匀，这个度量称为差异（discrepancy），差异有许多形式，其中的一种称为星差异（star discrepancy），它的定义如下：

$$D^{*}_n=D^{*}_n(x_1,\cdots,x_n)=\sup_{a\in[0,1)^d}\bigg| \cfrac{1}{n}\sum^{n}_{i=1}1_{0\leq x_i<a}-|[0,a)|\bigg|$$

（式16）

$\cfrac{1}{n}\sum^{n}_{i=1}1_{0\leq x_i<a}$表示的是盒子内的采样占总采样数量的比例，所以星偏差（偏差的一般形式定义中盒子$[a,c)$中的$a$和$c$可以取任意值，而不是一个固定在原点的盒子$[0,a)$。}表示的是在所有盒子$[0,a)$中，盒子体积与其盒子内点所占总数比例的差的绝对值的最大值。图（6）展示了这种偏离度的概念，它包含一个固定在原点的盒子$[0,a)\in [0,1)^2$以及一个$n=20$的序列，盒子里面有4个点，所以$(1/n)\sum^{n}_{i=1}1_{0\leq x_i<a}=0.2$，而盒子的体积为$0.6\times 0.25=0.15$，所以其差为$|0.2-0.15|=0.05$，星偏差$D^{*}$是取所有盒子$[0,a)$的最大值。

图（6）：图为在一个单位正方形内的20个点组成的序列，以及一个固定在原点的盒子，$a=(0.25,0.6)$，盒子的体积为0.15，占据的点的比例为$4/20=0.2$。

有了序列的偏差度的数值定义，我们可以用它来分析序列的均匀性对估计错误程度的影响。拟蒙特卡洛估计的错误被其使用的序列的偏差限定在一个有界区间内，更精确地讲，Koksma–Hlawka不等式（The Koksma–Hlawka inequality）声明拟蒙特卡洛估计的错误（这里的错误定义和方差是有一点区别的，估计值和期望值之差的绝对值才是估计错误的真实形式，而方差的定义为了避免绝对值带来的麻烦而使用错误平方的期望形式表示。）：

$$\epsilon=\Bigg| {\rm \int}_{[0,1]^{d}f(\mu){\rm d}\mu}- \cfrac{1}{N}\sum^{N}_{i=1}f(x_i) \Bigg|$$

（式17）

被限定在区域：

$$|\epsilon |\leq V(f)D^{*}_{N}$$

（式18）

之内。这里的函数$V(f)$为被积函数$f$的Hardy-Krause方差（Hardy-Krause variation），该不等式可以用于展示拟蒙特卡洛估计的错误边界为$O( \cfrac{(\log{N})^{d}}{N})$，而传统蒙特卡洛估计的错误为$O( \cfrac{1}{\sqrt{N}})$。虽然我们只能声明拟蒙特卡洛估计错误的上边界（upper bound）值，但实践上拟蒙特卡洛方法的收敛速度要比理论上快得多，因此一般情况拟蒙特卡洛方法比传统的蒙特卡洛方法的收敛速度要快；此外，从该表达式也可以看出拟蒙特卡洛估计的维数$d$越小，其估计错误越小，收敛速度越快，

低差异序列

产生低差异序列的方法和伪随机数序列的方法是完全不同的。产生多维伪随机数序列的间接方法是首先由伪随机数发生器（如系统中的random(u)函数）产生一维随机数序列，然后根据概率论定理，用间接方法（如逆向变换算法，取舍算法等）将一维伪随机数序列转换为多维伪随机数序列；然而拟随机数不是随机的，而是确定的，没有概率统计特性，因此不能像产生多维伪随机数那样的方法工作。

因此我们使用直接方法产生多维拟随机数序列。直接方法即是数论方法，数论方法是基于数论中的一致分布理论，利用数论中关于整数，素数，同余式等知识产生多维拟随机数序列。数论当中有许多方法用于产生低差异序列（low-discrepancy sequence）的方法，本节我们仅讨论比较常用的几种利用倒根函数实现的低差异序列。

倒根函数

任何一个自然数$i=0,1,2,\cdots,n$可以展开为以$b$为底的正幂次的表达式，即是用$b$进制表示自然数$i$，其中$b$称为基（radix），其展开式为：

$$i=\sum^{m-1}_{l=0}a_l(i)b^{l}$$

（式19）

其中，$a_l(i)$为数字展开式的系数，$m$为数字展开式的项数，$m$决定了$i$在$b$进制下的位数，它允许展开$N=b^{m}$个自然数，例如数字123用10进制表示为$123=3\cdot 10^{0}+2\cdot 10^{1}+1\cdot 10^{2}$。如果我们将展开系数$a_0,a_1,\cdots,a_{m-1}$看成一个$m$维的向量，则该展开式将一个自然数序列转换成了一个多维的向量序列。

有了这个多维向量序列，为了将它转换为$[0,1]^d$空间的向量序列，首先需要将该序列转换为$b$进制的小数形式，这就需要用到倒根函数（radical（此处radical实际上是取名词radix的形容词形式，因此理解为"根的，基的"意思，和"base"的意思是一致的，因此倒根函数指的是对基进行反向映射，由$b$进制映射回10进制。） inverse function），倒根函数表示将该序列转换为以$b$为底的负幂次的表达式，即是$b$进制的小数形式，其定义如下：

$$\Phi^{-1}_{b,C}(i)=(b^{-1}\cdots b^{-m})\begin{bmatrix} C \begin{pmatrix} a_0(i)\\ \vdots\\ a_{m-1}(i) \end{pmatrix} \end{bmatrix}$$

（式20）

其中，$C$是一个生成矩阵（generator matrix），生成矩阵通常和底数的选择有关，每个低差异序列算法中的不同点就在于底数$b$和生成矩阵$C$的选择。

有了$b$进制小数形式的多维拟随机向量，最后一步直接将该向量转换为10进制即可，以上的过程就将自然数$0,1,2\cdots,n$一共$n$个数转换为$n$个$[0,1]^{m}$空间上的向量序列，即是我们最终需要的拟随机数序列。以下我们简单介绍两种基于倒根函数生成的低差异序列。

科普特序列

科普特序列（van der Corput sequence）是一维的拟随机数序列，其一维底数$b$可取任一素数，$C$为单位矩阵。例如以底数2为例，图（7）列出了16个拟随机数组成的特普特序列，由于$C$为单位矩阵，所以正幂次的2进制形式在转换为负幂次的2进制形式的时候，相当于将每个展开系数的顺序反转，如图（7）中的第二，三列所示。

图（7）：16个拟随机数的一维科普特序列，其中底数$b$为2，$C$为单位矩阵，科普特序列主要就是靠反转二进制形式的各个位的顺序来获得。

霍尔顿序列}

另一个常用的低差异序列是霍尔顿序列（Halton sequence），霍尔顿序列是科普特序列扩展到高维的一般形式，即是霍尔顿序列的生成矩阵$C$也是单位矩阵，但是霍尔顿序列的底数选择方式不一样，一维的霍尔顿序列就是底数为$2$的科普特序列。

霍尔顿序列的每维有不同的底数，霍尔顿序列第$j$维的底数是第$j$个素数，即维数取值$j=1,2,3,4,5,6,7,8,9,10,\cdots$，对应维数的霍尔顿序列底数取值为$b_j=2,3,5,7,11,13,17,19,23,29,\cdots$，根据数论中的判别素数的相关方法可以得到自然数素数表。

图（8）：256个伪随机数序列和开头256个Halton(2,3)序列中随机数的均匀性比较（图片来自Wikipedia）

由于数字展开式$a_l(i)\in \{1,2,\cdots,b_j-1 \}$，而霍尔顿序列的底数随维数增加而增加，所以当维数$j$越高，底数$b$就越大，系数$a_l$个数就越多，计算循环时间越长。此外，由于高维使用的底数是比较大的素数，循环会很长，出现一些空隙结构，所以霍尔顿序列的均匀性在10维以上逐渐变坏，出现丛聚现象，20维以上丛聚就比较明显了，所以并不适合高维的拟随机数序列。

有很多低差异序列用于改善高维霍尔顿序列的退化现象，这里不再详述，相比这些序列，霍尔顿序列的而优势在于生成矩阵$C$为单位矩阵，而其他低差异序列往往有着非常复杂的生成矩阵，计算复杂度大大增加，所以在低维情况下霍尔顿序列几乎是最好的选择。