1.4 采样和反走样

3D图像的生成本质上是一个对各种连续函数（如几何图形，BRDF分布函数，光照场等）采样，然后转化为对应的一个离散函数（以有限分辨率表示的一个二维图像）的过程。3D渲染的大部分采样发生在光栅化阶段，或者其他由光栅化导致的采样，例如第1.3节图（11）中，三角形两个顶点之间的边是连续的，但是被光栅化过程采样为离散的像素值。

在数字信号处理（digital signal processing）中，术语采样（sampling）的目的是将连续的信号表述为离散的信号，在采样的过程中，其中的一些信息会丢失；为了重建（reconstruction）原始连续信号，则需要对离散信号使用过滤（filtering）技术来还原原始连续信号，如图1所示。

图（1）：在数字信号处理的过程中，一个连续的信号(左图)被采样为离散的信号（中图），然后通过重建还原为接近原连续信号的连续信号（右图）

以下我们就首先来讨论采样和重建这两个数字信号处理的基本过程，然后介绍一些由于采样不足导致的走样的概念以及其一般解决方案。

采样

关于采样的理论非常复杂，它涉及傅里叶变换，积分，级数等数学知识，以及像频率域等滤波相关的概念。然而理解采样相关知识是理解走样相关知识的重要理论基础，而且在图形学的其他一些地方也会涉及这些知识，例如在光线追踪技术中就会大量涉及脉冲函数。此外，理解傅里叶变换也有助于理解后面的如小波变换，球谐函数等概念。但本节不会严格地推导和讨论傅里叶相关的知识，而只是使用一些结论让读者比较容易地理解采样相关的概念及逻辑，本书后面的内容还会反复更深入地讨论傅里叶变换相关的知识，更多关于数字图像处理的理论知识，可以参考[cite b:DigitalImageProcessing]。

法国数学家傅里叶（Jean Baptiste Joseph Fourier）于1807年在他的《热分析理论》一书中指出，任何非周期（但该曲线下的面积是有限的）的连续函数可以用正弦和/或余弦乘以一个加权函数的积分来表示，这个积分方程称为傅里叶变换（Fourier transform）。用 $F(\mu)$ 表示连续变量 $t$ 的连续函数 $f(t)$ 的傅里叶变换，则：

F(\mu)={\rm \int}^{\infty}_{-\infty}f(t){\rm e}^{-j2\pi\mu t}{\rm d}t

（式1）

其中， $\mu$ 表示正弦项或余弦项的频率，由于被积函数中的变量 $t$ 被积分，所以上式的结果为变量 $\mu$ 的函数。

周期函数

对于任何周期函数则可以使用傅里叶级数，表示为不同频率的正弦和/或余弦和的形式，每个正弦项和/或余弦项乘以不同的系数。例如具有周期 $T$ 的周期函数 $f(t)$ 的傅里叶级数为：

f(t)=\sum^{\infty}_{n=-\infty}c_n {\rm e}^{j \cfrac{2\pi n}{T}t}

（式2）

其中：

c_n= \cfrac{1}{T}{\rm \int}^{T/2}_{-T/2}f(t){\rm e}^{-j \cfrac{2\pi n}{T}t}{\rm d}t, n=0,n=\pm 1,n=\pm 2,\cdots

（式3）

相反，给定 $F(\mu)$ ，通过傅里叶反变换可以获得 $f(t)$ ：

f(t)={\rm \int}^{\infty}_{-\infty}F(\mu){\rm e}^{j2\pi\mu t}{\rm d}\mu

（式4）

利用欧拉公式 ${\rm e}^{j\theta}=\cos\theta +j\sin\theta$ ，可以把式（1）表示为：

F(\mu)={\rm \int}^{\infty}_{-\infty}f(t)[\cos (2\pi\mu t)-j\sin(2\pi\mu t)]{\rm d}t

（式5）

我们看到，由于变量 $t$ 被积分后只剩下 $\mu$ ，所以傅里叶变换 $F(\mu)$ 的作用域是频率域。频率变量 $\mu$ 的单位取决于 $t$ 的单位，例如，如果 $t$ 表示单位为秒的时间，则 $\mu$ 的单位为周/秒，如果 $t$ 表示单位为米的时间，则 $\mu$ 的单位为周/米。

从广义上讲，频率域（frequency domain）表述的是一个连续函数在它的作用域上的改变有多快，所以一个函数通常有多个频率，这些频率构成该函数的一个频率谱（spectrum of frequencies）。傅里叶变换正是将一个连续非周期函数由其时间域（如果一个信号随时间而变化，称该作用域为时间域。）（time domain）或空间域（例如与时间无关的静止的图像，它的作用域为空间位置 $x,y,z$ ，称为空间域。）（spatial domain）变换到其频率域。其目的在频率域我们可以发现该函数的一些重要特征，甚至一些对函数的操作在频率域进行更方便。

从图2中可以看到这种作用域的转化，红色线条代表原始连续周期函数（注意这里是针对傅里叶级数而非傅里叶变换进行描述），蓝色线条为傅里叶级数各级的正弦或余弦函数，图2(a)包含了傅里叶级数的头6项，这个傅里叶级数本身是有无穷多项的。图2(b)通过提取出每个正弦或余弦项的频率，而形成图2(c)的频率域函数，这个频率域将用于后面对信号采样的质量判定。值得注意的是，由式2可知，其傅里叶级数的频率域是离散的；然而由式（1）可知，非周期连续函数的频率域函数，即傅里叶变换函数是连续的，如图3所示。

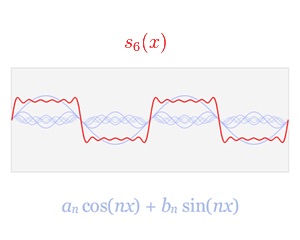
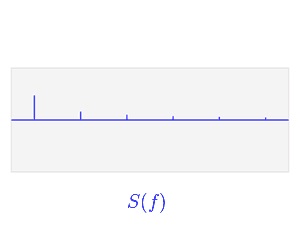
图（2）：傅里叶变换将函数由时间域（或空间域）变换到频率域，注意这里讨论的是周期函数的傅里叶级数（图片来自Wikipedia）

当一个函数被变换到频率域后，则我们可以检测该函数是否存在最大的频率，以至对于所有大于该频率的傅里叶变换函数的值为 $0$ 。如果该最大频率存在，该函数称为带限函数（bandlimited function），这意味着我们可以检测该函数的频率带宽（bandwidth），如图3是某个函数的傅里叶变换，其频率带宽为 $2B$ 。带限函数是后面对函数进行采样以及相关理论的重要基础概念。

图（3）：一个带限函数的频率域具有一个有限的范围，如果采用频率大于这个带限的宽度，则其采样后的离散信号可以被完美复原（图片来自Wikipedia)

为了理解采样及采样定理，我们需要首先了解一下卷积的概念，卷积在计算机图形学中也是一个重要的基础数学工具，例如在后面讨论渲染方程，以及一些全局光照方案中几乎所有涉及球谐函数（spherical harmonics）的地方等都会涉及卷积，所以本节首先学习卷积及其在傅立叶变换中的应用。

卷积

在数学上，卷积（用符号 $\star$ 表示）定义为两个函数 $f$ 和 $g$ ，在其中一个函数被翻转 $180^{\circ}$ 之后（以下假设 $g$ 被翻转），两个函数乘积的积分，即：

f(t)\star g(t)={\rm \int}^{\infty}_{-\infty}f(\tau)g(t-\tau){\rm d}\tau

（式6）

注意这里 $\tau$ 是一个积分假变量，它说明在积分滑过整个定义域的同时，翻转函数 $g$ 将作用于 $f$ 的每一个位置。

我们可以给卷积做一个很直观的视觉解释，在图4中，蓝色曲线表示函数 $f$ ，红色曲线表示函数 $g$ ，以下过程可以用来描述卷积的计算：

图4：卷积的视觉解释，对于两个函数 $f$ 和 $g$ 的卷积（第一行），我们首先将 $g$ 执行 $180^{\circ}$ 翻转（第二行），然后将 $g(t-\tau)$ 从定义域的左边（第三行）开始向右滑动（第四，五行），并在每个位置 $t$ 处计算式（6）中的积分（图片来自Wikipedia）

对函数 $g$ 执行 $180^{o}$ 翻转： $g(\tau )\to g(-\tau )$ ，如图4第一行到第二行的图形变化。
设置一个时间偏移 $t$ ，使 $g(t-\tau )$ 从 $\tau-$ 轴的起点位置开始“滑行”，如图4第三行所示。
将 $t$ 从 $-\infty$ 滑动到 $\infty$ ，即是将 $g$ 从 $-\infty$ 沿 $\tau-$ 轴滑动到 $\infty$ 经过整个时间域，如图4第四和五行所示，只要两个函数存在相交，则计算它们乘积的积分，换句话说，在每个时间 $t$ ,对 $f(\tau )$ 执行一个权重系数为 $g(-\tau )$ 的积分，注意式（6）的积分变量为 $\tau$ ，它表示被执行翻转的函数 $g$ 的作用域，所以整个积分是一个关于 $t$ 的函数，我们需要求解每个 $t$ 处的积分。

这个过程形成的关于 $t$ 的波形（在图中没有画出），即是 $f$ 和 $g$ 的卷积。由此可以看出，卷积计算是对 $f$ 整个定义域的每一点，在 $g$ 定义域内的积分计算。因此卷积的计算量非常大，我们看到后面的一些计算中， $g$ 的定义域一般都非常小。此外，卷积是一个线性计算，它输出一个和 $f$ 定义域一样大小的结果，例如，如果 $f$ 代表的是一张图像，则卷积计算的结果输出另一张一样大小的图像。另外，卷积公式本身只是关于每个点 $t$ 的计算公式，所以卷积实现必须要遍历整个 $f$ 定义域。

对于卷积和傅里叶变换，可证明（读者可参考[cite b:DigitalImageProcessing]等相关书籍），空间域中两个函数的卷积的傅里叶变换等于两个函数的傅里叶变换在频率域的乘积；反过来，如果有两个变换的乘积，则可以通过计算傅里叶反变换得到空间域的卷积，这即是卷积定理（convolution theorem）。换句话说， $f(t)\star h(t)$ 和 $H(\mu)F(\mu)$ 是傅里叶变换对，这一结果是卷积定理的一半，可以写为：

f(t)\star h(t)\Leftrightarrow H(\mu)F(\mu)

（式7）

双箭头用于指示右边的表达式是通过对左边的表达式执行傅里叶变换得到的，而左边的表达式是通过求右边表达式的傅里叶反变换得到的。

遵循类似的推导可得到卷积定理的另一半：

f(t)h(t)\Leftrightarrow H(\mu)\star F(\mu)

（式8）

它说明频率域的卷积类似于空间域的乘积，两者分别与傅里叶正，反变换相联系。卷积定理是傅里叶分析的重要基础，也是计算机图形学中很多算法的重要基础工具。

采样定理

有了傅里叶变换和卷积定理两个基础工具，我们就可以推导出采样定理，由于信号处理涉及对连续信号进行采样，以生成离散信号，然后通过离散的采样结果对函数进行重建的过程，采样定理告诉我们，在什么条件下可以完美地重建原始连续信号。除此之外，采样定理还能帮助我们理解走样的概念，以及对离散信息进行平滑等知识。

首先我们需要了解冲激函数（dirac function）的概念，它是推导采样定理的重要基础。连续变量 $t$ 在 $t=0$ 处的单位冲激表示为 $\delta(t)$ ，其定义为：

\delta(t)=\begin{cases} \infty & t=0\\ 0 & t\neq 0 \end{cases}

（式9）

同时它还被限制为满足：

\int^{\infty}_{-\infty}\delta(t){\rm d}t=1

（式10）

很容易看出，假设函数 $f(t)$ 在 $t=0$ 处是连续的，那么冲激函数具有如下的采样特性：

\int^{\infty}_{-\infty}f(t)\delta(t){\rm d}t=f(0)

（式11）

更一般地，对于任意位置 $t_0$ 处的冲激函数 $\delta(t-t_0)$ ，采样特性变为：

\int^{\infty}_{-\infty}f(t)\delta(t-t_0){\rm d}t=f(t_0)

（式12）

可以看出，冲激函数的采样特性可以简单地得到冲激位置处的函数值，那么如果我们定义一个具有均匀间隔的冲激串函数，将这个冲激串作用于一个连续函数，那么其结果就得到对原始信号的均匀采样。

一个具有均匀间隔 $\Delta T$ 的冲激串函数可以定义为：

s_{\Delta T}(t)=\sum^{\infty}_{n=-\infty}\delta(t-n\Delta T)

（式13）

上述冲激串表述的函数如图5(b)所示。将上述冲激串函数作用于一个连续函数 $f(t)$ ，则得到以下采样后的函数为：

图（5）：冲激函数具有采样的能力，它可以简单地得到冲激位置处的函数值，所以函数$f(f)$的均匀采样可以定位为使用一个冲激串函数(b)与之相乘，这得到采样过后的函数(c)，最终每个冲激位置处的采样值由加权后的冲激强度给出(d)

\tilde{f}(t)=f(t)s_{\Delta T}(t)=\sum^{\infty}_{n=-\infty}f(t)\delta(t-n\Delta T)

（式14）

上述和式的每一个分量都是由在该冲激位置处 $f(t)$ 的值加权后的冲激，如图5(c)所示。每个采样的值由加权后的冲激“强度”给出，我们可以通过积分得到它，即任意采样值 $f_k$ 为：

f_k=\int^{\infty}_{-\infty}f(t)\delta(t-k\Delta T){\rm d}t=f(k\Delta T)

（式15）

图5(d)显式了上述的采样结果，它由原始函数的等间隔采样而成。

为什么要用这么复杂的方式来表述函数采样呢？这是因为借助冲激函数的傅里叶变换以及卷积定理，我们可以得出采样定理，并进而指导我们对函数进行采样。

令 $F(\mu)$ 表示连续函数 $f(t)$ 的傅里叶变换， $\tilde{F}(\mu)$ 为采样后的函数 $\tilde{f}(t)$ 的傅里叶变换，由卷积定理可得：

\tilde{F}(\mu)=\Im\{\tilde{f}(t)\}=\Im\{f(t)s_{\Delta T}(t)\}=F(\mu)\star S(\mu)

（式16）

其中， $\Im$ 符号表示傅里叶变换， $S(\mu)$ 为冲激串函数的傅里叶变换：

S(\mu)=\cfrac{1}{\Delta T}\sum^{\infty}_{-\infty}\delta\bigg(\mu -\cfrac{n}{\Delta T}\bigg)

（式17）

可以看出，冲激串函数的傅里叶变换仍然为一个冲激串函数，这是一个非常重要的特性，由此我们可以得到采样后的函数 $\tilde{f}(t)$ 的傅里叶变换为：

\begin{aligned} \tilde{F}(\mu)=&F(\mu)\star S(\mu)={\rm \int}^{\infty}_{-\infty}F(\tau)S(\mu-\tau){\rm d}\tau\\ =&\cfrac{1}{\Delta T}{\rm \int}^{\infty}_{-\infty}F(\tau)\sum^{\infty}_{n=-\infty}\delta\bigg(\mu-\tau-\cfrac{n}{\Delta T}\bigg){\rm d}\tau\\ =&\cfrac{1}{\Delta T}\sum^{\infty}_{n=-\infty}{\rm \int}^{\infty}_{-\infty}F(\tau)\delta\bigg(\mu-\tau-\cfrac{n}{\Delta T}\bigg){\rm d}\tau\\ =&\cfrac{1}{\Delta T}\sum^{\infty}_{n=-\infty}F\bigg(\mu-\cfrac{n}{\Delta T}\bigg) \end{aligned}

（式18）

其中，上式的第一行使用了卷积的基本定义，即两个函数的卷积等于它们乘积的积分，仍然需要注意的是，上述卷积中的翻转函数 $S(\mu)$ 会在每个 $\tau$ 处作用于整个函数 $F(\tau)$ 的定义域上，而由于 $S$ 是一个冲激串函数，我们把 $\cfrac{1}{\Delta T}$ 项提到外面，就产生了一个神奇的结果，即它在每个位置处将 $F(\mu)$ 复制一次，而复制的间隔由 $1/\Delta T$ 决定。很明显，虽然采样后的函数 $\tilde{f}(t)$ （在空间域）是离散的，但是其傅里叶变换 $\tilde{F}(\mu)$ （在频率域）却是连续的，因为它由 $F(\mu)$ 的几个拷贝组成，而 $F(\mu)$ 是连续的。

图（6）显示了上述这种采样后函数的傅里叶变换图示，其中图（6）(a)为原始连续带限函数 $f(t)$ 的傅里叶变换，图（6）(b)~(d)则表示采样后函数的傅里叶变换，如前所述， $1/\Delta T$ 是用于生成采样后函数的采样率。由此可以看出，为了保持对原始信号的重建能力，我们需要使用足够的采样率来保证 $F(\mu)$ 的完整性，在图（6）(c)中，采样率刚好能够保持 $F(\mu)$ ，因此我们可以使用一个低通过滤器（如图中的虚线线段所示）来完全得多原始信号的所有频率信息，因此能够被完美重建，这部分的内容将在下一节讨论。而在图（6）(d)中，采样率低于保持不同 $F(\mu)$ 拷贝的最小采样率要求，因此它无法被完美重建。

图6：(a)为一个带限函数的傅里叶变换，(b)-(d)分别为过采样，临界采样和欠采样条件下采样后函数 $\tilde{f}(t)$ 的傅里叶变换 $\tilde{F}(\mu)$

在图6(d)中，由于采样后函数的周期变小，因此各个拷贝的相邻位置处发生重叠，如图6(d)的红色线段部分所示，这部分的频率信息表现为相互叠加部分的和（这是因为式（18）是各个拷贝的和式），即这部分的频率信息被修改，因此发生了走样（aliasing）。实际上alias这个单词的意思是别名，这里的本意实际上是指某些频率信息被其他的频率值代替。可以想象，此时使用能够覆盖一个周期的低通过滤器，是不可能完全保留原始函数的所有频率信息的，因此无法被完美复原。

由此可知，当一个连续函数被采样成一个离散函数之后，其能够被重建为原函数的能力取决于采样点的密度（density of samples），或称为采样率（sample rate）。根据采样理论（the sampling theorem），对于一个带限函数 $f(t)$ ，其最大的频率为 $\mu_{\rm max}$ ，它能够完全被一系列以 $1/(2\mu_{\rm max})$ 间隔采样的离散函数表示。换句话说，采样率必须大于或等于 $2\mu_{\rm max}$ 采样点/秒，或者说对于一个采样率 $f_s$ ，其原始连续函数能够被完美复原的条件是： $\mu_{\rm max}<f_s/2$ 。

当频率带宽 $\mu_{\rm max}$ 太高（或者该函数完全不存在频率带宽），则这种不完美的复原导致的结果就是走样（aliasing）。这两个临界值 $2\mu_{\rm max}$ 和 $f_s/2$ 称作奈奎斯特采样率（Nyquist rate）和奈奎斯特频率（Nyquist frequency）。由该采样定律定义的不等式条件称为奈奎斯特准则（Nyquist criterion）。采样理论又称为奈奎斯特-香农采样定理（Nyquist–Shannon sampling theorem）以纪念Harry Nyquist和Claude Shannon对其的贡献。

关于对离散函数的重建过程及其方法将在下一节讨论，采样的不足将导致走样的产生，本节最后将分析几种计算机图形学中涉及的一些比较重要的走样，通过对这些走样现象的分析和了解，将有助于更好地理解采样率对图像质量的影响。

几何走样

回到第1.3节（感应器）讨论的由于光栅化导致的三角形的走样，如图（11）所示，对于光栅化，我们按照屏幕的分辨率对几何图形的可见性函数（visibility function）进行采样，即采样点之间的间距为一个像素，采样点的位置为每个像素的中点。

可见性函数是一个连续函数，要想最终呈现很高质量的图像，必须要在图像上还原出很好的原始可见性函数，根据采样定律，必须要使用2倍于可见性函数最高频率的采样率。然而，三角形的可见性总是存在不连续，这种不连续性导致无限大的频率，从而使其傅里叶变换不存在有限的频率带宽，因此没有任何采样率可以阻止这种走样发生；另外根据傅里叶变换的条件，只有定义域在无限的时间域或空间域才能使其傅里叶变换具有有限的频率带宽。所以对于计算机图形学中有限的二维或三维空间域，走样现象是不可避免的。

这种由于对几何图形的可见性函数采样导致的走样称为几何走样（geometric aliasing），它是计算机图形学中最严重的走样现象，因为整个场景图像的渲染都是根据物体表面的的位置来决定的，而每个像素点的位置都是光栅化阶段对物体几何形状的可见性函数来决定的。

虽然没有任何采样率可以有效地避免几何走样的存在（即完美地对可见性函数采样），但是我们仍然会寻求一些方法来减轻这种走样现象，其中比较流行的方法称为过采样（oversampling），详见重采样一节，这种方法本质上使用比图像分辨率更高的采样频率对原始可见性函数进行采样，然后使用这些采样点来重建像素对应的采样率下的函数值。这在3D渲染中相当于使用高于图像输出分辨率的频率渲染场景，然后将其缩放至输出分辨率，这个过程称为超采样（supersampling）。本章后面全屏反走样将详细讨论这种技术。

着色走样

着色走样（shader aliasing）发生于像素着色器中，它和纹理走样有点类似，也主要是由于像素着色器受限于屏幕分辨率所限导致的。然而不同的是着色走样主要是指，在着色器中对一些以分析的方式得到的连续函数的采样不足导致的走样，而不是对纹理的采样不足。

这类走样比较严重的例子是对粗糙度比较低的光泽表面的采样，由于表面低粗糙度导致其光泽分布范围更狭窄，如第1.3节图（9）所示，从而导致光泽BRDF分布函数具有更高的频率，因而更容易导致走样。当对物体表面使用法线贴图后，这种走样现象更明显，因为法线导致物体表面的光泽具有更高的频率。

对于着色走样，其不可能通过后面全屏反走样节介绍的MSAA技术解决，因为MSAA对于每个像素的着色只计算一次（但对Depth和Stencil值取多个采样点），所以它对着色走样没有任何影响；超采样（supersampling）虽然可以减少这类走样，但是其代价太高，并且提升效果不是很明显。如图（7）表示在有法线和光泽反射的情况下，三种不同方法的渲染结果。

图（7）：该图显示光泽和法线条件下，不同方法对着色走样的处理：左图正常绘制，走样现象比较严重，尤其注意在法线频率变化比较大的区域，信息丢失比较严重，中图使用4倍的超采样，右图使用一种直接基于法线计算光泽反射的方法，该方法能得到更好的结果（图片来自\cite{m:ApplyingSamplingTheorytoReal-TimeGraphics}）

对于渲染方程中由于粗糙度，法线以及其他相关因素导致的采样问题，比较有效的解决思路是，首先将这些参数融入到光照计算（例如后面讲述的微面元BRDF理论）中去，使这些“原始连续函数”更平缓，然后再对这些光照计算结果采样，这样的思路在本书后面的一些内容中有介绍。

时间走样

前面的例子都是对处于空间域的2个 $(x,y)$ 或者3个 $(x,y,z)$ 连续变量进行采样，然而在游戏或者电影动画渲染中，由于大量的物体处于运动状态，因此，对于另一个时间域的采样问题也特别突出。

时间走样（temporal aliasing）出现于当物体在运动时，由于渲染帧率的限制使其对运动过程的采样不足导致的走样。游戏画面的渲染是根据帧率按较低的采样率对时间域进行采样，所以对于高速运动下的物品，其时间域的频率较高，很容易出现走样。其中一个比较经典的例子称为车轮效应（Wagon-wheel effect），它使一个旋转的辐条车轮表现出不同的视觉效果，例如轮子可能看起来比实际更慢，或者看起来像静止一样，甚至沿着相反的方向旋转。

为了减轻时间走样，一种比较常用的方法称为运动模糊（motion blur）。这种方法跟超采样一样，它依靠对时间域取更多的采样点，然后对其进行反走样，当然这种方法的计算成本很高。另一种更普遍的方法是针对当前帧渲染结果，生成一个速率缓存（velocity buffer）[cite a:AReconstructionFilterforPlausibleMotionBlur]，然后使用这些方向在后处理阶段对其邻近的像素点执行插值计算，如图（8）所示。

图（8）：使用速率缓存实现运动模糊，图中左上表示当前帧的原始渲染结果，左中为深度缓存，左下为速率缓存，右图为最终结果

重建

重建（reconstruction）是指将采样后的离散函数还原为原始连续函数的过程，为了从一些离散的采样点还原为原始连续函数，必须对离散函数执行一个滤波器（filter）。“滤波”一词源于数字信号处理中，用于在频率域上接受（通过）或拒绝一定的频率分量。然而滤波器实际的概念非常复杂，根据滤波器是离散还是连续，以及被滤波器作用的函数是离散还是连续，滤波器的作用以及实现的结果都是不一样的。

平滑

根据卷积公式的特性，我们可以很容易想到它可以用来平滑函数 $f$ ，然而不仅如此，根据卷积计算是作用在时间/空间域或者频率域，以及 $f$ 和 $g$ 是离散还是连续函数，它表现出来的功能特征和结果是不一样的，以下我们就分别来描述卷积的这些应用场景。

卷积计算最本质也是最直观的特征是平滑，它通过对 $f$ 的每个点考虑该点周围一定范围内的值对该点的影响，来消除该点与周围环境的频率的快速变化。这在计算机图形学中运用十分广泛，大部分可能出现走样的地方，例如前面采样一节讨论的那些走样现象，都可以在采样之前对原始函数进行平滑，以减轻走样现象。这种滤波器称为反走样滤波器（anti-aliasing filter）。

这里举一个图像处理的例子，在图像处理中，常常考虑 $f(x,y)$ 为一个具有一定分辨率的图像， $g(x,y)$ 为一个 $m\times n$ 的矩形，其分辨率通常小于或等于 $f(x,y)$ 的分辨率，假设 $m=2a+1$ 且 $n=2b+1$ ，其中 $a,b$ 为正整数，则式（6）变为：

g(x,y)\star f(x,y)=\sum^{a}_{s=-a}\sum^{b}_{t=-b}g(s,t)f(x-s,y-t)

（式19）

可以看出，卷积的意义相当于使用一个 $m\times n$ 的模板 $g$ ，以它的中心从 $f$ 的每一个像素点经过，对于每一个像素点，分别计算模板上对应位置的两个函数乘积的和，如图（9）所示，其卷积输出为一个新的与 $f$ 分辨率相同的图像。

图（9）：在图像处理中，卷积的意义相当于使用一个蒙板遍历每一个像素点，分布计算蒙板内所有乘积的和，GPU中纹理过滤相关的技术都是通过卷积的方式实现

重建

除了平滑，借助卷积的特性还可以实现将离散函数还原为原始连续函数，卷积的这种运用称为重建滤波器（reconstruction filter）。重建的操作表现为用一个无限连续的 $g$ 作用于采样后离散的 $f$ ，然而为了直观理解重建的过程，我们需要首先从频率域以及采样定理说起。

前面已经介绍过采样定理相关的内容，设 $\tilde{F}(\mu)$ 为对 $f(t)$ 采样后的离散函数 $\tilde{f}(t)$ 的傅里叶变换，如图（10）(a)所示，为了使 $f(t)$ 能够被完美重建，首先需要保留 $\tilde{F}(\mu)$ 所有的频率，在本例子中使用了一个高于奈奎斯特采样率的频率进行采样。如果能够从 $\tilde{F}(\mu)$ 中包含的这个函数的拷贝的周期序列中分离出 $F(\mu)$ 的一个拷贝，那么我们就可以从采样后的版本恢复 $f(t)$ 。

图（10）：盒状滤波器通常用来在频率域对信号进行重建

为了从原理上了解如何从 $\tilde{F}(\mu)$ 复原 $F(\mu)$ ，在图（10）(b)中 $H(\mu)$ 的定义如下：

H(\mu)=\begin{cases} \triangle T & -\mu_{\max}\leq\mu\leq\mu_{\max}\\ 0 & \text{其他} \end{cases}

（式20）

当乘以图（10）(a)中的周期序列时，该函数就隔离了以原点为中心的一个周期，然后通过 $H(\mu)$ 和 $\tilde{F}(\mu)$ 相乘得到 $F(\mu)$ ：

F(\mu)=H(\mu)\tilde{F}(\mu)

（式21）

一旦得到了 $F(\mu)$ ，就可以通过傅里叶反变换来复原 $f(t)$ ：

f(t)={\rm \int}^{\infty}_{-\infty}F(\mu){\rm e}^{j2\pi\mu t} {\rm d}\mu

（式22）

以上这些公式从理论上证明了，以函数包含的最高频率的两倍的速率采样得到的函数的样本，来恢复一个带限函数是可能的。

上述的函数 $H(\mu)$ 称为一个低通滤波器（low-pass filter），因为它通过频率范围低端的频率，并且消除所有较高的频率。所以要想完美复原原始函数，原始函数 $(f(t))$ 必须是带限函数。

对式（21）利用卷积定理，可以在空间域得到等价的结果，即：

f(t)=\Im^{-1}\{F(\mu)\}=\Im^{-1}\{H(\mu)\tilde{F}(\mu) \}=h(t)\star\tilde{f}(t)

（式23）

可导出 $f(t)$ 的如下空间域表达式（此处略去证明过程，请参考[cite b:DigitalImageProcessing]等相关书籍）：

f(t)=\sum^{\infty}_{n=-\infty}f(n\triangle T) {\rm sinc}[(t-n\triangle T)/\triangle T]

（式24）

这相当于对离散函数使用一个辛克函数（sinc function）（如图11所示）的卷积，辛克函数的定义如下：

{\rm sinc}(x)= \cfrac{\sin (\pi x)}{\pi x}

（式25）

这并不奇怪，因为盒装滤波器 $H(\mu)$ 的傅里叶反变换就是一个辛克函数。

图（11）：蓝色曲线表示归一化的辛克函数，而红色曲线表示未归一化的辛克函数，在计算机图形学中一般使用归一化的版本（图片来自Wikipedia）

我们不禁要问，卷积主要用来平滑一个离散或者连续函数，那它是怎样实现这种类似于在样本点之间插值的效果的呢？这里主要是由于辛克函数是在无限空间连续的，所以当它划过 $\tilde{f}(t)$ 上的每一点时，会在辛克函数的整个定义域上求积分，因为积分值是一个标量，即该点的卷积总是可能具有一个值，并且这个值其实是考虑 $\tilde{f}(t)$ 所有点的平滑效果而得来的，因此它能完美还原 $f(t)$ ，同时实现了使用卷积来重建一个离散函数。当卷积被这样使用时，称之为重建过滤器（reconstruction filter）。

在图像处理中，重建过滤器主要有两个用途：第一种为上面讲述的从一个采样过的离散函数重建原始连续函数，另一种称为重采样（见下一节），即在纹理被缩小或者放大时，调整图像的分辨率。这两种场景本质上都是把滤波器看做一种计算某个特定的点的插值的工具，即我们并不需要对一张图像全部像素点做卷积计算，而是找出另外一些当前这些采样点之外的点的值。

然而，式（24）要求样本间的内插有无限多项，在实际中，这意味着我们必须找到一种样本间内插有限的近似方法，在图像处理中使用的主要内插方法是最近邻法，双线性法和双三次内插法，这些插值方法将在下一节讨论。

重采样

在渲染场景的时候，程序会大量使用预先采样的数据，如图像，或者场景的某些离散的表示空间结构数据等。这些数据都是具有一定的分辨率（或者是按一定的采样率生成的数据），当程序中需要在不同分辨率下使用这些数据时（例如摄像机靠近或者远离表面导致纹理被放大或者缩小），我们需要对这些离散的数据进行重采样（resampling），以生成一个具有不同分辨率的数据。以下我们主要以GPU中对纹理的采样分析分辨率转换的问题。

当摄像机靠近物体表面时，即发生放大操作（magnification），这使摄像机能看到更多细节，它要求对原始函数使用更高的采样率采样。如图12所示，这要求生成更多的采样点，根据上一节讲述的内容，我们只需要对于离散的图像提供一个滤波器，便可以对任意点进行插值。

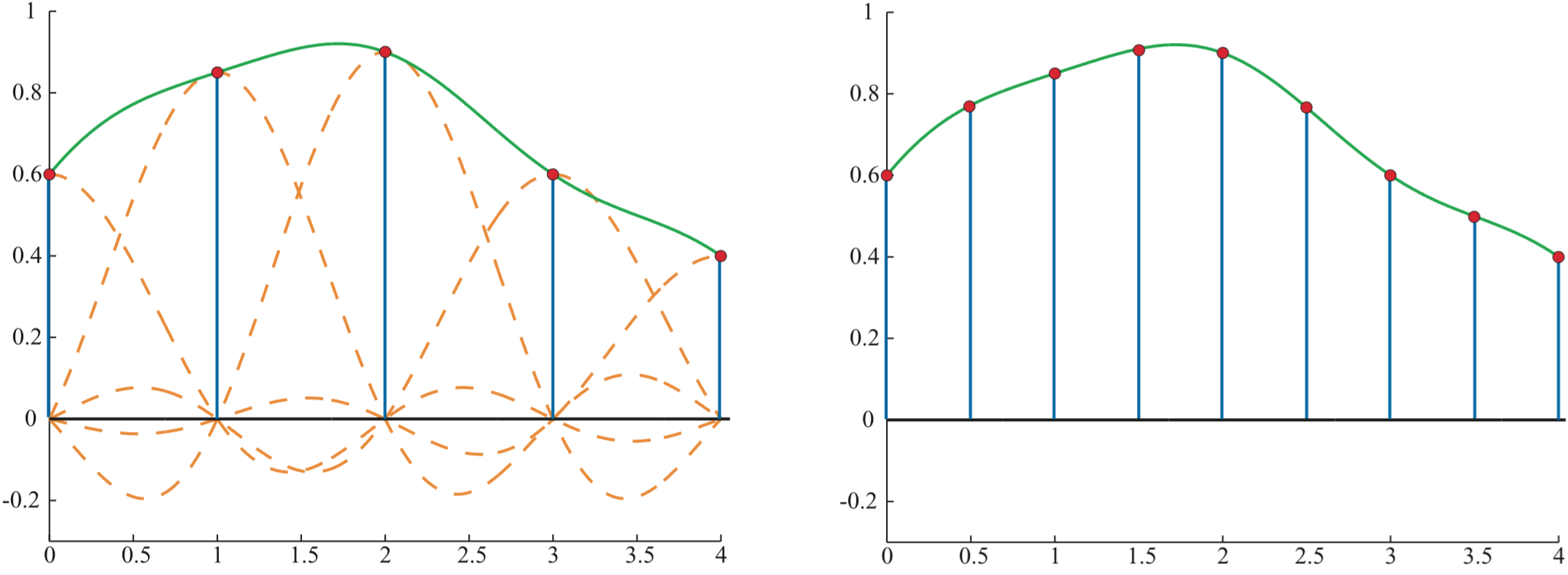
图（12）：左图的原始经过采样的离散信号，当摄像机靠近物体上需要对信号进行放大操作（图片来自\cite{b:rtr}）

然而，正如前面提到的，辛克函数要求样本间的内插值有无限多项，所以我们必须使用一些近似方法来进行插值计算。最简单的方法是最近邻插值（nearest-neighbor interpolation），它采用像素复制的放大操作。例如，将一幅图像放大两倍，我们可以复制每一列，这会在水平方向上将图像尺寸放大一倍；然后复制这幅放大后图像的每一行，在垂直方向上将图像尺寸放大一倍。相同的步骤可用于任意整数倍放大图像。最近邻内插法实际上是对图像使用一个盒式过滤器（box filter），如图13所示。

图（13）：最近邻内插法直接选择离重建点最近的样本值作为内插值（图片来自Wikipedia）

双线性插值（bilinear interpolation）法则分别基于采样点的位置在 $X$ 和 $Y$ 轴上线性地插值，如图14所示。双线性插值法本质上对图像执行一个三角形过滤器（triangle filter）或称为篷形过滤器（tent filter）。

图（14）：双线性插值法分别基于采样点的位置在$X$和$Y$轴上线性地插值（图片来自Wikipedia）

双线性插值法仅仅考虑采样点周围的4个 $2\times 2$ 像素点，双三次内插法（bicubic interpolation）则考虑周围16个 $4\times 4$ 像素点，可以给出更平滑的插值结果（最近邻插值法和双线性插值法都会使还原的函数具有导数不连续的点，即导致非常高的频率变化，从而导致走样比较严重）。双三次内插法使用的滤波器函数如下：

W(x)=\begin{cases} (a+2)|x|^{3}-(a+3)|x|^{2}+1 & $for $|x|\leq 1 \\ a|x|^{3}-5a|x|^{2}+8a|x|-4a & $for $1<|x|<2 \\ 0 & 其他 \end{cases}

（式26）

这里 $a$ 通常取值-0.5或者-0.75，注意 $W(0)=1$ ，对于所有非0整数 $W(n)=0$ 。双三次函数具有如图15所示的形状。

图15：双三次内插法考虑周围16个 $4\times 4$ 像素点，可以给出更平滑的插值结果（图片来自Wikipedia）

全屏反走样

在采样一节讨论了几种形成走样的原因，其中的几何走样和着色走样这两种比较明显的走样是和分辨率有关的，所以如果我们能够从像素着色器（pixel shader）来解决走样的问题，或许我们能够解决所有由于分辨率带来的走样（注意，前面提到过着色走样并不能通过本节所讲述的MSAA技术减轻走样，本节稍后将会分析其原因。）。本节基于屏幕空间的反走样技术正是基于这样的思路，并且它通常是由硬件在渲染管线中直接实现的反走样技术，因此不对任何具体渲染实现有什么影响。

在开始讨论具体的全屏反走样技术之前，首先我们应该思考的是，对于固定的屏幕分辨率（相当于固定的采样率），其反走样的思路是什么。通过前面对采样及滤波器等知识的学习，我们知道走样是一个采样问题，它不能通过任何技术手段在采样之后消除这种由采样不足导致的走样。那么走样是什么，走样是由于采样率低导致傅里叶变换的高频部分被修改，从而使高频区域出现较大的误差。所以，在固定采样率的前提下，我们能做的事情就是对原始函数进行平滑，消除原始函数的高频部分，即减少了频率宽度，而这可以通过低通过滤器来实现（回想重建一节滤波器的主要功能是通过卷积实现平滑）。

然而，在渲染中，我们通常并不能对原始函数进行平滑，一方面存储这样的原始函数（例如几何图形的可见性函数）需要大量的内存；另一方面，平滑是一个相对的概念，例如一个图像数据的频率对于 $1920\times 1200$ 的分辨率来说是平滑的，但是它对于 $1024\times 640$ 的分辨率来说频率带宽仍然太宽。这就是为什么纹理缩小时需要使用多级纹理（mipmap）技术而不是直接从原始图像进行缩放。

根据以上这些分析，过采样（oversampling）就是一种针对特定分辨率的反走样技术，它通过使用一个比输出分辨率略高的采样率对原始函数进行采样，并对这个高分辨率的样本函数使用滤波器进行平滑（重建），然后对这个高分辨率的样本函数进行重采样得到输出分辨率的图像。

过采样又称为超采样（supersampling），它是一种对每个像素点计算多个子采样点（subsamples）的反走样技术。其最简单的形式称为全屏反走样（full-scene antialiasing，FSAA），FSAA对场景以一个更高的分辨率进行渲染，然后对相邻的采样点取平均值得到最终图像，例如对于一个 $1000\times 800$ 分辨率的图像，首先使用 $2000\times 1600$ 的分辨率对场景进行渲染，然后对每个 $2\times 2$ 的样本面积求平均值得到最终图像。这种技术的特点是实现非常简单，但是其计算成本很高，每一个子采样点都需要被使用完整的渲染管线进行着色。

图（16）：根据实现不同，FSAA对子样本点使用不同的采样模式（图片来自Wikipedia）

对于FSAA，需要注意的是，可以对每个像素范围内的子采样点采用不同的分布，图（16）介绍了其中几种采样模式（关于采样模式，我们将在第[ref chp:mc]章介绍更多的细节。）（sampling pattern），不同的采样模式具有不同的优点，例如RGSS对像素格子按规则的采样模式进行渲染，然后将样本进行旋转，这样得到的结果使得接近水平线的变化更加平坦，实际上，[cite a:Jaggededges:whenisfilteringneeded?]指出人的眼睛对接近水平或垂直直线的走样更敏感，而对 $45^{o}$ 左右直线的走样敏感度是最低的；Nvidia的高分辨率反走样（high-resoulution antialiasing，HRAA）¹使用Quincunx的采样模式，它对每个像素点使用两个子采样点，但是使用Quincunx的分布模式，使得每个像素可以使用周围的4个（一共5个点）相邻的子采样点进行平均求值。当然这里只列出少数几种采样模式²。

超采样技术对每个子采样点的着色，深度及位置等都需要进行单独的计算。对于由几何图形光栅化导致的走样，实际上我们只需要对其可见性函数进行采样即可，即是说我们可以将可见性函数从着色当中分离出来，这样对于每个像素点只需要计算一次着色（即执行一次像素着色器），这样将大大减少反走样的计算量。基于这样思路的反走样技术称为多重采样反走样（multisample antialiasing，MSAA）。然而其代价是由于每个像素的颜色只计算一次，因此它不能实现着色走样的反走样，这仍然需要借助多级纹理等技术来实现。

MSAA需要借助图形API的光栅化技术来实现，在图形渲染管线的光栅化阶段，光栅化器根据输入的几何图形的顶点，按照输出分辨率将几何图形光栅化成一个个像素点，然后对每个像素点执行一个像素着色器以计算该像素颜色，深度，模板值，其中像素着色器只计算颜色值，而深度值由光栅化器计算，模板值则应用程序对图形接口的调用来决定。而在一个实现MSAA的光栅化器，它会对每个像素生成多个子采样点，并计算每个子采样点的深度和模板值，而对于颜色值，光栅化器对每个像素只调用一次像素着色器，然后将计算结果复制给每个子采样点。

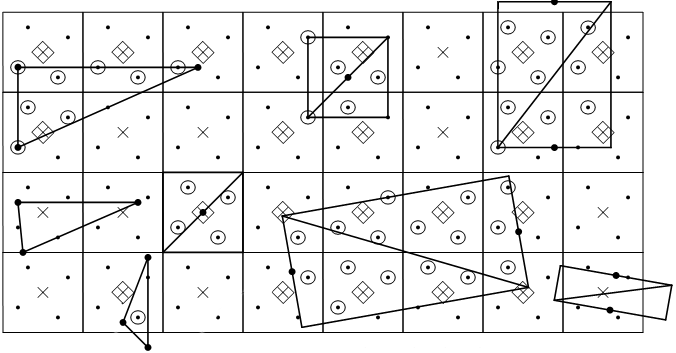
图17：DirectX 11中MSAA的实现，其中 $\cdot$ 为子采样点的位置， $\bigcirc$ 为几何图形覆盖的子采样点， $\diamond$ 为像素着色器执行颜色计算的位置（图片来自MSDN）

图17为DirectX 11中MSAA的实现，对于每个通过深度和模板测试的子采样点，其深度和模板值将被写入到缓冲区，该子采样点的颜色值由像素着色器计算，最后该颜色将被乘以该像素点的覆盖率，覆盖率是由几何图形所占区域中所有可见的子采样点与总采样点之比。

在上述的光栅化过程中，像素着色器根据像素点中心的位置从纹理采样，以计算该像素的颜色值，然而如果几何图形只占据像素点的一小部分，则中心点不会被覆盖到，从而导致从纹理中不正确的位置获得颜色值。为了保证颜色计算的正确性，这个像素着色器使用的采样位置可以被调整到覆盖区域中某个点的位置，这种技术称为质心采样（centroid sampling），或者质心插值（centroid interpolation）。对于一个被几何图形覆盖的像素点，它首先从像素中心点开始寻找，如果中心点没被几何图形覆盖，则一次向外延伸直到找到一个被覆盖的子采样点，该点的位置将作为最终像素着色器对纹理采样的位置。

MSAA相对于超采样大大减少了计算量（每个像素着色器只执行一次计算），然而MSAA并没有减少内存占用，CSAA[cite m:CoverageSamplingAntialiasing]则进一步将像素点的覆盖率从颜色/深度/模板值当中分离出来，使其内存占用和数据传输的宽度占用都得到降低。

图18：一个 $16\times$ CSAA的颜色和覆盖率存储结构，该设置使用4个子采样点，但是使用16个位置来计算其覆盖率，使得覆盖率数据更精准

如图18所示，除了MSAA中的子采样点，CSAA还使用了一个二进制结构的数组蒙板（bit mask）表示覆盖率，这个覆盖率比子采样点具有更高的分辨率，在光栅化阶段，光栅器首先投影几何图形到该蒙板以计算覆盖率，然后对子采样点进行采样计算深度，模板及颜色值，其中计算颜色值的时候其覆盖率直接由该蒙板提供。这样使得更少的子采样点可以得到更精准的覆盖率，而原本这需要更多的子采样点来存储这些数据，而每个子采样点存储深度，模板及颜色值，所以在存储占用及数据传输带宽占用方面都是很大的。

关于覆盖率与深度，模板及颜色值的分离，其思路来源于[cite a:TheA-bufferanAntialiasedHiddenSurfaceMethod]中的A-buffer技术，图形学中还存在大量从分离覆盖率着手的解决方案。本节仅对全屏反走样技术做基本的介绍，更多的反走样技术还涉及与渲染方法（例如延迟着色）结合起来工作，所以我们需要在接触相关的概念之后才能进行深入地学习，后面还会更深入地讨论各种各样的反走样技术。

采 样​

卷 积​

采样定理​

几何走样​

着色走样​

时间走样​

重 建​

平 滑​

重 建​

重采样​

全屏反走样​

Footnotes​

采样

卷积

采样定理

几何走样

着色走样

时间走样

重建

平滑

重建

重采样

全屏反走样

Footnotes