1.3 物体的表面着色

在了解了全局光照应该实现各种物理现象，以及模拟自然光照计算需要的一些基本物理度量之后，从本节开始，我们将开始进入计算机图形学的世界。

正如前言所述，本书除了介绍计算机图形学的一些基本理论知识，另一个重要的目标是试图解释清楚这些理论知识之间的逻辑联系，本节的目标是在没有涉及具体的全局光照方法之前，尝试解释光与物体的交互过程，以及最终怎样被渲染成图像。在本节的末尾，我们仍然会通过这种高层抽象的物体表面着色需求（而不是从基础的数学公式），推导出渲染方程的表达式。然后在第[ref sec:intro-the-rendering-equation]节，将会更详细地解释渲染方程。

几何光学模型

本节首先介绍光的一些基础物理特征，这些特征是我们模拟真实的光与物体交互的基础，从而能够渲染出更真实的图像。

在电磁学中，有两种模型用于研究光的性质，第一种为物理光学，第二种为几何光学。物理光学（physical optics），又称为波动光学（wave optics），它认为光在介质中以波的形式传播，这种模型可以解释光的衍射和干涉等现象。然而它以光的波长为测量尺寸，这大大超出了计算机图形学的需求。

由于可见光的波长非常短，另一种模型忽略光的波长，即相当于$\lambda\to 0$的极限情况，并证明（感兴趣的读者可以参考书籍[cite b:PrinciplesofOptics]第三章的推导。）在这种近似处理下，光学定律可以用几何学的语言来描述，这种模型称为几何光学（geometric optics），或者称为光线光学（ray optics），因为这种模型下能量可以看作是沿着直线传输。几何光学模型正是被计算机图形学广泛采用的模型。

当然，几何光学模型仍然比较复杂，在计算机图形学中，我们作出了一些简化假设，这虽然限制了一些效果如衍射，但是它处理起来相对简单，并且满足一般图形学的需求。这些假设包括：

• 物体的表面是绝对光滑（真实世界的物体表面不是绝对光滑的，它的粗糙度介于光的波长和一个像素的尺寸之间，这种粗糙度可以通过下一节介绍的微面元技术实现，它本质上是反射和折射的一种聚合。）（smooth）的。
• 光仅可以被发射（emitted），反射（reflected）或者传播（transmitted）。
• 光以无限快的速度沿直线传播。

在这些假设下，光的反射由反射定律（law of reflection）决定，即： 给定一条入射光线$\mathbf{l}$和表面法线$\mathbf{n}$，反射光和入射光处于同一个平面, 并且反射光与法线之间的夹角大小等于入射光与法线的夹角大小，如图1所示。

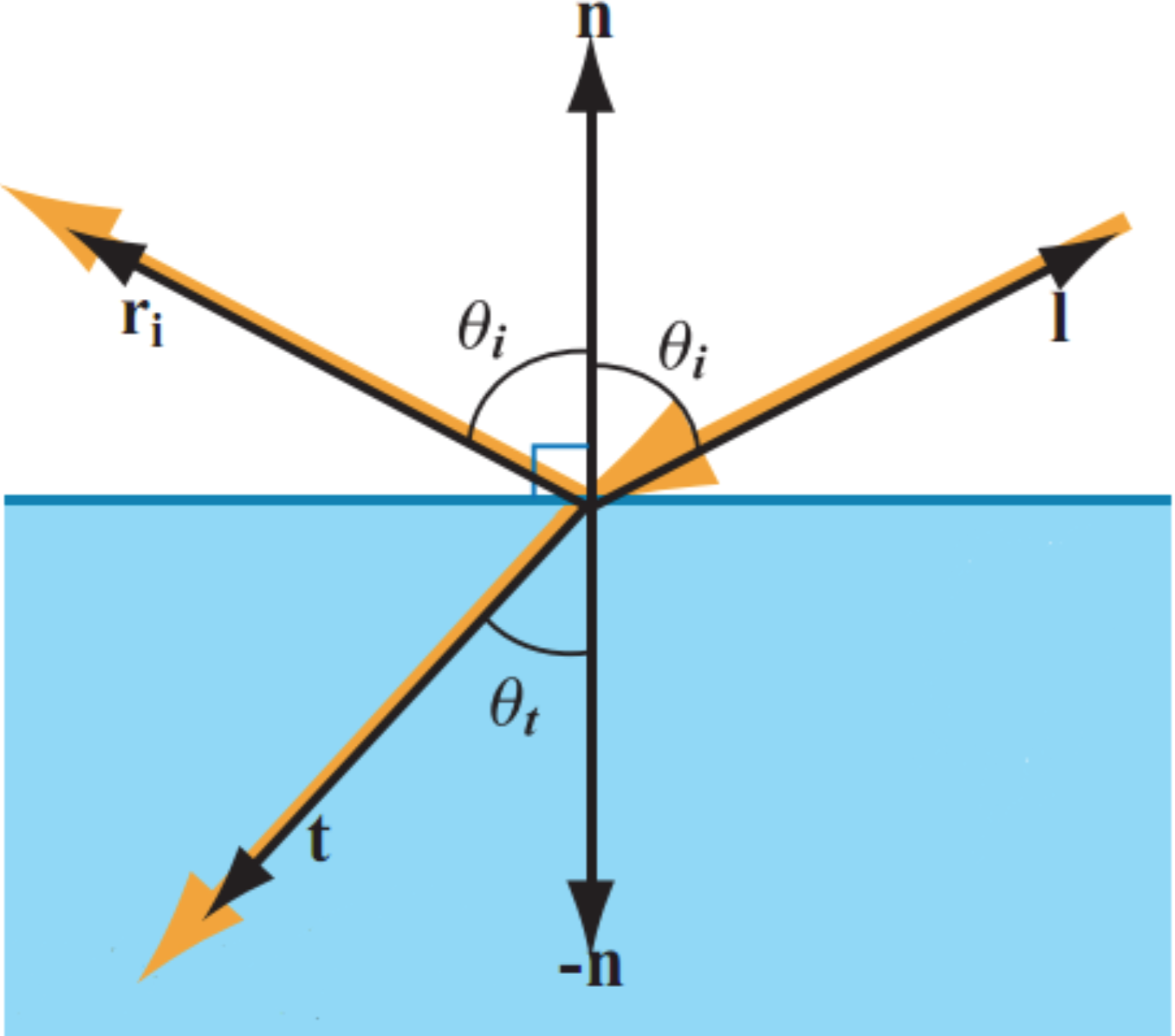
图（1）：在几何光学模型中，反射定律和斯涅尔定律决定光的反射和折射

当光在传输过程中，介质的折射率（index of refraction）发生变化，则会发生折射（refraction）。当入射光$\mathbf{l}$从具有折射率为$n_1$的介质进入折射率为$n_2$的介质时， 其光线传输方向的偏离$\mathbf{t}$由斯涅尔定律（Snell's law）决定，如图1所示，即有：

$$n_1\sin\theta_1 = n_2\sin\theta_2\$$

（式1）

光与表面的交互

为了模拟光学现象以生成真实的数字图像，我们需要构建一套系统，将几何光学模型应用到计算机图形学中。这套系统定义了在图形渲染过程中，光与表面及其他物体的交互。

这个系统工作的过程可以描述如下：

• 光从光源（例如太阳或其他光源）或其他发光体中发射出来。
• 光与场景中的物体进行交互，部分被反射，部分被吸收并可能经过一定路径传播后沿其他方向从物体表面散射出来。
• 最后，光被感应器（例如摄像机或者人的眼睛）吸收，形成图像。

这个过程涉及三个组件：光源，材质以及摄像机。在接下来的小节中我们将讨论这些组件，以及它们怎样被用在渲染管线中用于渲染图形。

光 源

光源（light sources）发出光并照亮整个场景，此外，在计算机图形学中，光源一般不会反射或吸收其他光照。

现实世界中的光源是很复杂的，它可能沿不同的方向以及光源表面上的不同位置具有不同的分布，在图形学中一般仅使用少数几种简单的光源模型，这几种模型都假设光源的光照分布只随方向而发生变化。这几种模型包括：

• 平行光（directional light）：平行光模拟光从无限远的地方发射，这意味着所有由它产生的阴影光线都是平行的，因此这种模型是模拟太阳光的理想选择。
• 点光源（point light）：点光源从一个点向四面八方发出光线，它可以用于模拟如现实世界中的钨丝灯泡发出的光。
• 聚光灯（spot light）：聚光灯限制点光源发出光线的方向，它通常使用两个圆锥体作为参数，其中内部圆锥体的半径内发出的光线最强，从内部到外部圆锥体半径内光线强度逐渐减至零。

以上这些光源发出的光线会在场景中像自然光一样进行传播，即这些光线通过最近点测试计算出光线与哪个物体表面的哪个位置相交，然后根据物体表面的材质属性进行着色计算。除此之外，出于性能考虑，场景中还有另外一些（通常是间接）光不会通过这种方式计算，例如大面积的环境光通常通过贴图的方式计算，这包括天空盒（sky light）以及其他环境光照；而低频率的间接漫反射的光可以通过使用低阶的球谐函数近似表述，然后在GPU中使用快速的卷积（convolution）计算。

对于直接光源，另一个我们最关心的问题是这个光源的光照用什么物理量表示，以及这个物理量怎样参与到光与表面的交互计算之中。

首先，虽然眼睛等感应器接收的是辐射亮度$L$，但这是一个五维（三个维度表示位置，两个维度表示方向）的量，太过于复杂，所以在图形学中一般不会直接表示光源的辐射亮度分布。考虑到图形学中大部分直接光源的亮度分布都是只与方向有关，所以辐射强度$I$通常用来表示本节提到的几种直接光源的辐射亮度分布。

当然这个方向分布函数不宜太复杂，一般引擎不允许定义具有任意方向分布的光源，例如点光源可能所有方向的辐射强度都相同，聚光灯也是沿着一个圆锥体向外递减。在Unreal Engine 4中，可以对点光源和聚光灯使用一个称为IES[cite m:IESLightProfiles] 的光源配置（light profiles）的配置文件。IES光源配置文件可以以曲线的方式定义光源的光照强度分布，如图2所示。

图（2）：在Unreal Engine 4中使用IES光源配置文件定义点光源和聚光灯的光照强度分布 （图片来自[cite m:IESLightProfiles）

通过第[ref sec:irradiance]节的内容可知，在计算光与物体表面交互时，表面接收的所有光照使用辐射照度$E$表示，而光源使用辐射强度$I$表示，所以这里就需要使用第[ref sec:irradiance]节介绍的的平方反比定律，通过$I$来计算$E$，为了方便，这里重新列出该方程如下：

$$E= \cfrac{I\cos\theta}{r^{2}}$$

（式2）

虽然$E$随着$1/r^{2}$正比增长在物理上是正确的，但是在图形学上通常使用一个不同的函数来描述$E$怎样随着距离的增加而递减。这种函数称为距离递减函数（distance falloff function），由此$E$可以表示为：

$$E=I\cos\theta f_{\rm dist}(r)$$

（式3）

距离递减函数在计算机图形学中被广泛采用，有以下一些原因：首先距离递减函数可以提供更多的控制来达到一些特殊的效果；其次，随着距离的增加，平方反比函数趋近于$0$但却永远不会为$0$，距离递减函数可以通过设定一个最大距离范围，超出这个范围的表面接收的辐射强度为0来大大提高性能；平方反比函数在距离趋近于$0$时趋近于无限大，而距离递减函数可以通过设定一个最大值，避免这种无限大的值出现在着色计算中。

例如以下是Pixar工作室用在电影产品中的距离递减函数[cite a:LightingControlsforComputerCinematography]：

$$f_{\rm dist}(d)=\begin{cases} M{\rm e}^{s( \cfrac{d}{L})^{\beta}}, & d<L\\ K( \cfrac{L}{d})^{\alpha}, &d>L \end{cases}$$

（式4）

这个函数在一个特定的距离$L$处其值为$K$，在距离小于$L$时逐步达到最大值$M$，递减指数$\alpha$用于控制当距离大于$L$时距离递减函数怎样随着距离递减，常数$s$和$\beta$被设定为特定值以保证函数在过渡点处的导数连续：其中$s\equiv {\rm ln}( \cfrac{K}{M})$，而 $\beta\equiv - \cfrac{\alpha}{s}$，如图3所示。

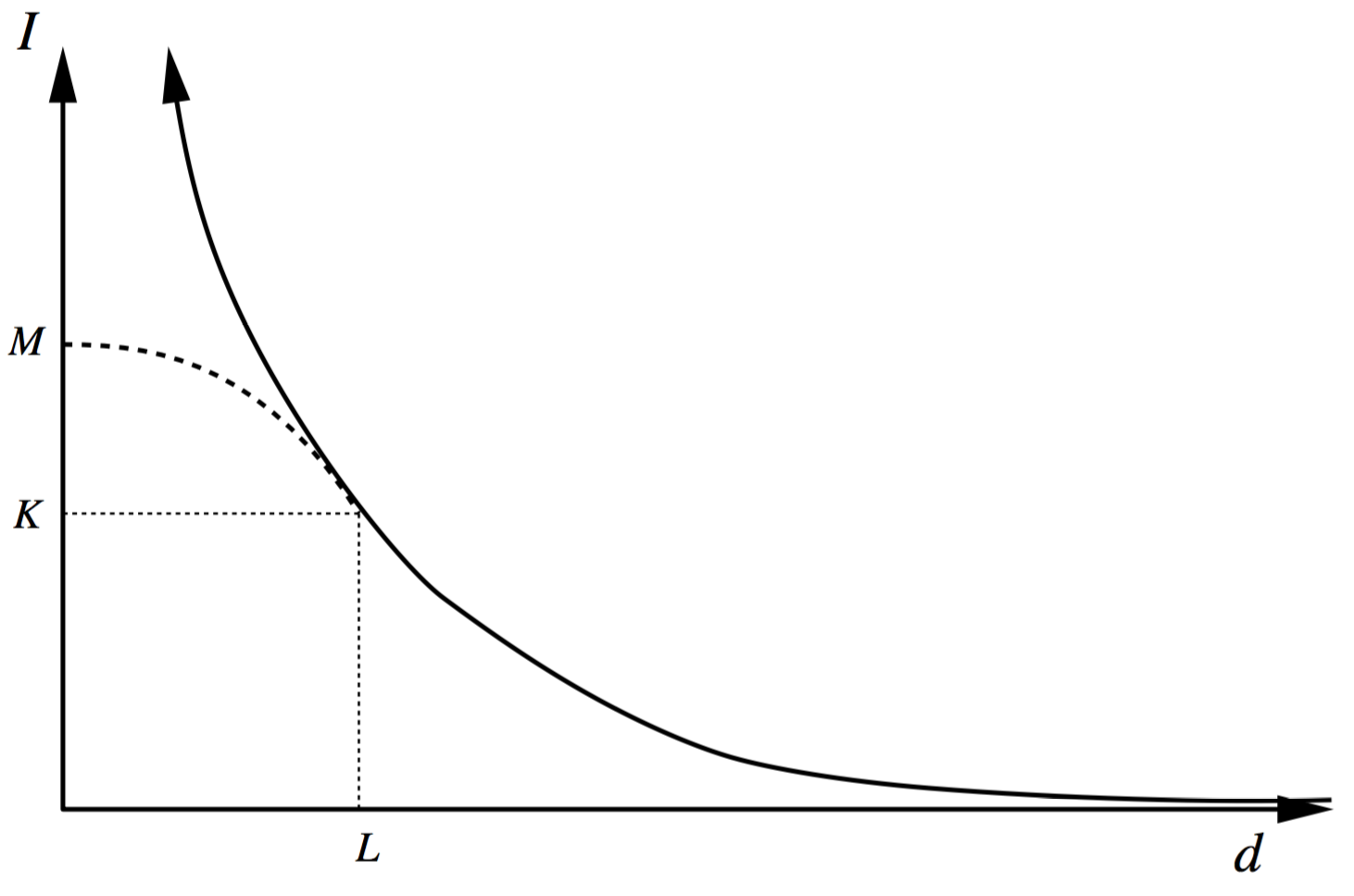
图3：Pixar采用的距离递减函数，其中当$d<L$ 时才有虚线部分，其最大值为$M$

材 质

光与物体表面交互的一切，都是由材质及其属性来决定的，材质决定了每个物体的表面最终呈现出来的是什么颜色。那么材质到底是什么，这个问题需要从两个方面来理解。

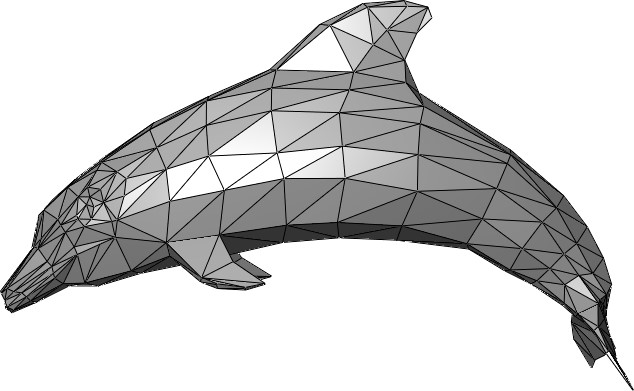
图（4）：一个由三角形网格构成的海豚，网格构成物体的“形”（图片来自Wikipedia）

首先，在计算机图形学中，一个物体的“形”与“色”是完全分开的，物体的形状由一组顶点（vertex）构成的网格（mesh）来定义，如图\ref4所示，而物体的表面着色则由称为材质（material）的东西决定。所以材质通常包含纹理（textures），着色器（shaders）以及其他一些着色方程需要的参数，所有这些数据构成一个对象并被附加到一个物体上，在渲染时这些数据被传输至GPU内存，GPU执行其中的着色器对该物体表面着色，这个过程包括贴图，光照以及其他相关的计算。关于材质的一些重要参数将在下一节讨论。

理解材质的另一方面在于，我们需要了解更多关于物体表面或内部结构的问题。在前面的描述中，都是假设表面是绝对光滑的，在这种情况下，光经过表面时按照反射定律和折射定律进行反射或折射。然而在微观尺度上（计算机图形学中一般不考虑小于波长的原子尺寸，这又称为纳米几何（nanogeometry），在此尺寸下可以观察到光的衍射现象，即光可以绕过障碍物沿非直线方向传播。），这里指微观几何（microgeometry）结构，即小于一个像素但是大于光波长的尺寸，物体表面并不是绝对光滑的，这时虽然在单个光束与表面交互上可以看作该面是光滑的，但是在一个像素尺度上，它却是不光滑的，如图5所示。那么我们如何处理这种复杂的情况？

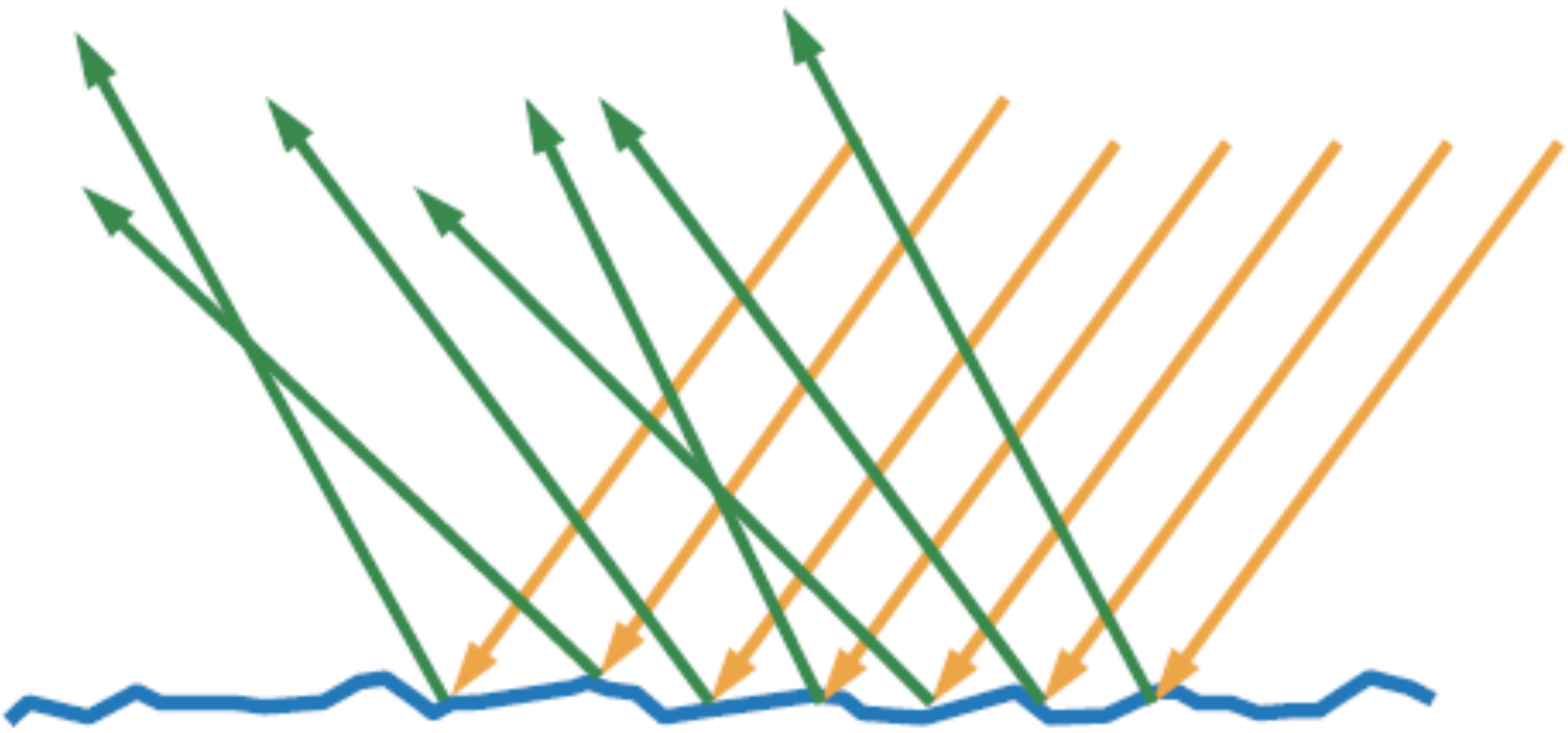
图（5）：在微观尺寸上，每个点向不同的方向反射或折射光照，注意该图反应的其实是一个像素内的微观尺寸

由于表面在微观尺寸上是不光滑的，每个比像素更小的点可能沿不同的方向反射或折射光照，这导致对于一个像素点，每条入射光会被反射或（和）折射至多个方向，如图6所示。这等效于是从一个给定的观察方向看，一个像素点可以接受来自多个方向的光照。

图（6）：微观结构的粗糙度，导致一个像素点可以将一束像素面积的入射光反射或（和）折射至多个方向

对于折射进物体内部的光照会发生什么呢，这取决于物体材质的结构。在计算机图形学中，材质可以分为两大类（自然界中还存在第三类材质，即半导体，但是半导体在渲染场景中很少见。）：金属（metals）和非金属，后者又称为绝缘体（insulator），其中金属立即吸收所有折射的光照。

对于非金属，如果该物体是透明的，如玻璃和水晶，则折射光会在物体内部直线传播，直到遇到该物体另一边的表面后离开物体表面重新回到空气中；对于非透明的物体，由于内部介质的不连续（例如流体，晶体等内部的粒子，泡泡，液滴，瑕疵；有机体表面的粗糙度，细胞；以及衣服布料里的纺织纤维等），折射的光会沿着不同的方向继续反射或者折射，在经历一定的路径之后，这些折射的光部分被重新（可能从原来的位置，也可能从其他位置）发射回到外面，部分可能被吸收。除非该物体是一个完全透明的物体，否则折射的光中总会有部分会发射回到表面外，如图7中的蓝色箭头部分光照，这部分光照可能从不同的位置以不同的方向发射出表面外。值得注意的是，这种由物体内部发射回来的光通常不具有固定的方向性，所以这种反射称为漫散射（scattering）。

图（7）：对于非金属材质，经历一定路径的散射之后，部分折射进表面的光会沿不同的方向重新发射回表面外

散射光重新发射回表面外的位置与入射点位置之间距离的分布，取决于该物质表面的属性。如果这个距离小于一个像素的尺寸（即在微观范围中），在着色的时候可以假设其距离为$0$，这种散射称为局部次表面散射（local subsurface scattering）；否则称为全局次表面散射（global subsurface scattering）。在计算机图形学中，这两种现象通常分别使用不同的技术实现。

在计算机图形学中，通常将反射和漫反射这两种不同的光照区分开，分别称为光泽（specular）和漫反射光（在光学中，漫反射（甚至散射本身）也包含一部分由于物体表面的粗糙度形成的直接反射光的一部分，并不全是由折射进表面的光形成。）（diffuse）。其中前者主要由于光在物体表面的直接反射形成，而后者通常由光进入物体表面，经历折射，吸收，多次散射过程之后重新从物体表面散射回表面外的光形成，如图8所示。这样区分的目的也在于由于漫反射光可以接收来自全部方向的光，因此需要对全空间进行积分计算，但是将与方向无关的部分分离出来，则可以使用更简单的方法处理漫反射，关于这些方法将在本章及本书后面介绍。

图（8）：光与物体表面交互后反射的光可以分为光泽和漫反射光两部分

对于光泽部分，这些反射光所处范围的大小取决于表面的粗糙度（下一节会讨论），表面越粗糙，则反射的范围越大，物体表面越模糊；反之表面越光滑，反射的范围越小，则表面越光亮，如图9所示。

图（9）：反射光的范围大小取决于物体表面的粗糙度，物体表面越粗糙，它越能接收更大范围的光照

由于材质决定物体表面的着色，所以上述所有这些现象都需要在材质中进行表述，对于如漫反射率等这种与观察方向无关的参数，它们可以通过纹理的方式存储并关联到材质中；而对于与方向有关的这些反射特征，它们可能以函数的形式存在于着色器代码中，例如上述关于表面的光泽反射特征可以通过本章后面介绍的微面元理论来进行表述。

感应器

当光从光源发射出，并在场景中与物体表面进行多次交互后，最终其中的一部分会进入图像传感器形成图像。由于图像传感器接收的是辐射亮度$L$（其值由渲染管线中的像素着色器计算出），并且数字图像以一定的分辨率存储图像信息，所以可以使用图10来表示计算机图形学中的图形传感器成像系统，这里$P$点就是场景中的“摄像机”对象，摄像机朝着虚拟屏幕中的每个像素的方向发射一条射线，称为观察矢量（view vector）$\mathbf{v}$（它也是着色器计算中渲染方程的出射方向），场景中所有沿$\mathbf{v}$反方向传播的光线就会进入摄像机。

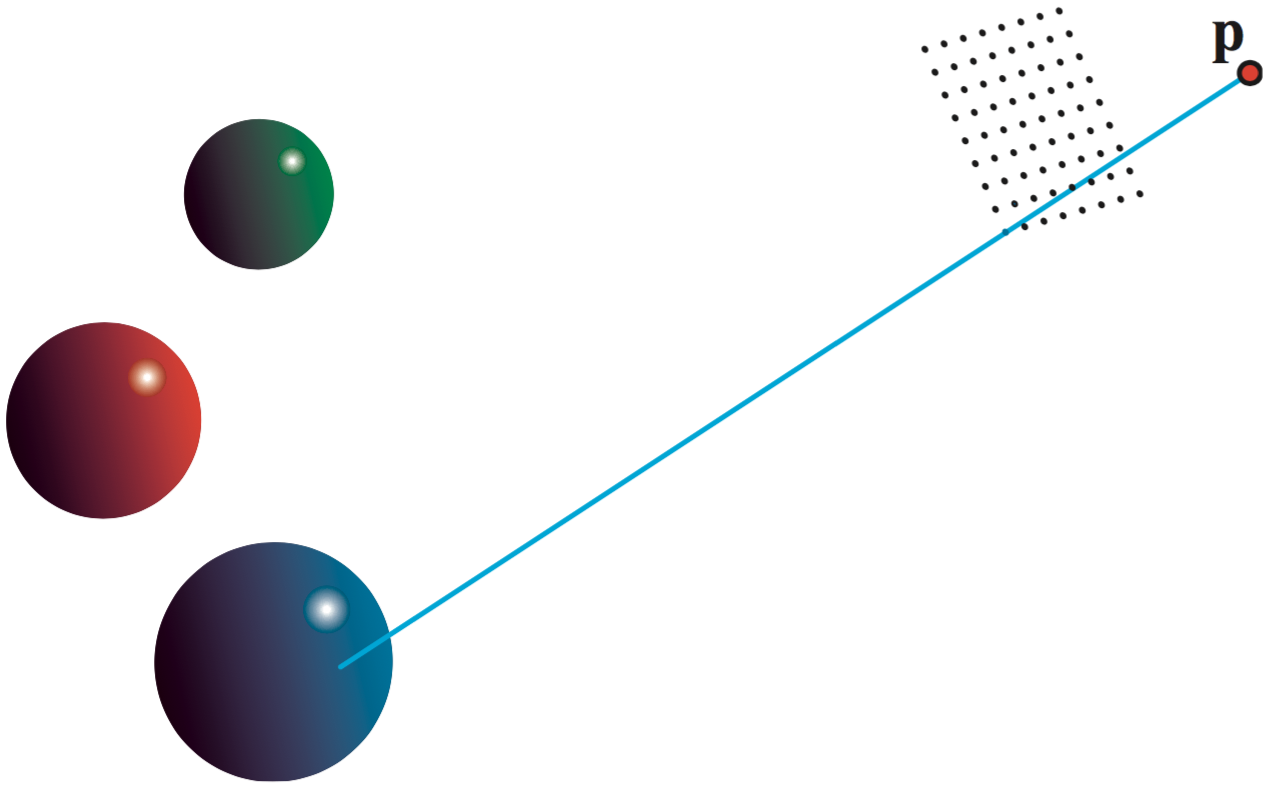
图10：理想的计算机图形学图像传感器模型，其中${\rm p}$为摄像机或观察点，中间的点阵为屏幕的像素网格，左边的球体为场景中的物体

然而事情并不像这么简单，对于给定分辨率的“屏幕”，它的每一个像素点总是有一个尺寸大小的。而对于每个像素，我们通常取其从摄像机发出穿过该像素中心点的方向对场景进行采样，如果一个像素的中心点被三角形覆盖，则整个像素区域被填充一个单一的颜色，否则即使该像素有小部分区域被覆盖，它也不会被填充任何颜色，这使得三角形的边缘出现锯齿（jaggies），如图11所示。这种锯齿是由于采样不足导致的一种走样（aliasing）现象,而尝试避免或者减少这种走样的技术称为反走样（anti-aliasing）技术。

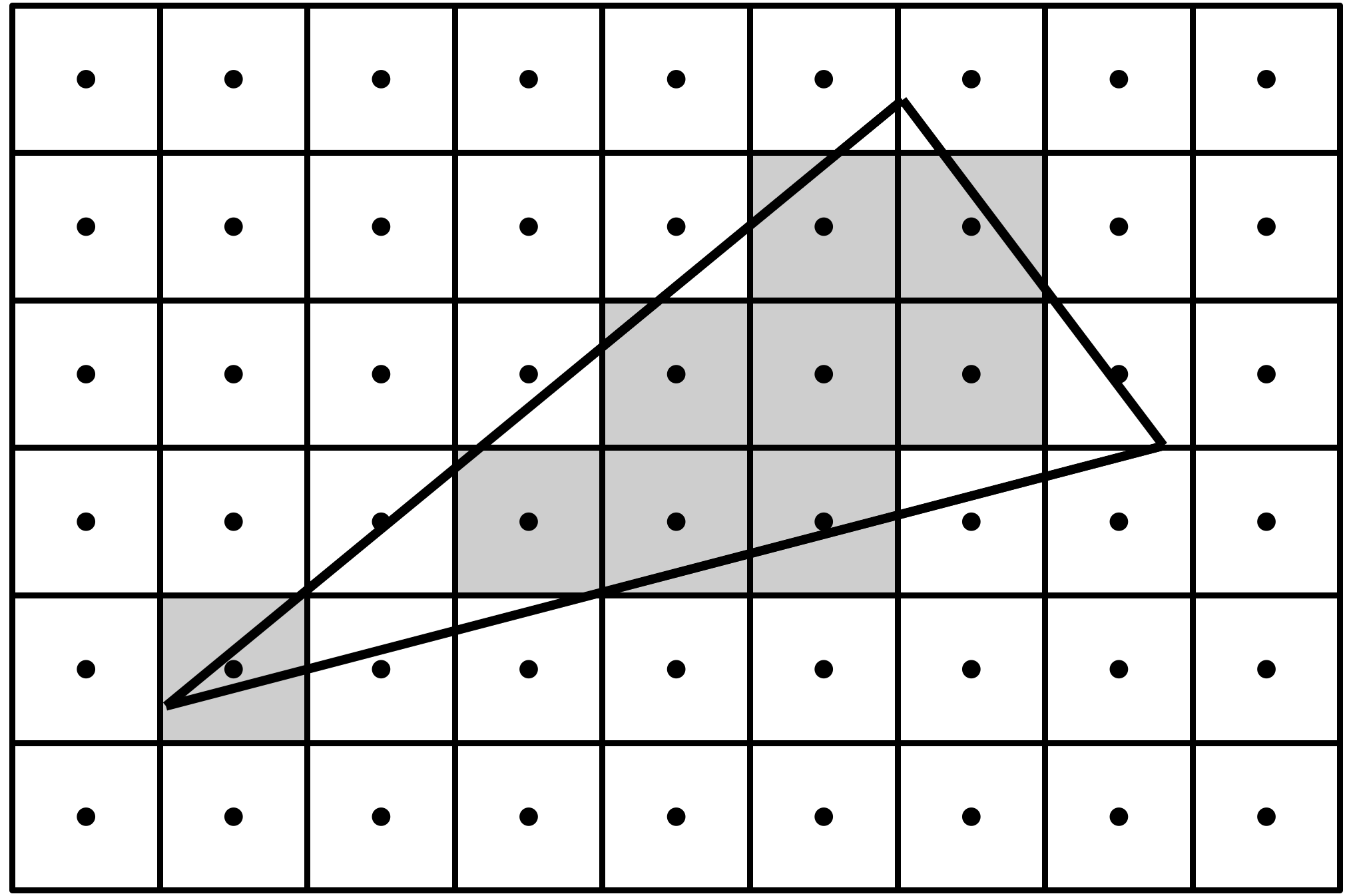
图（11）：光栅化技术通过测试几何图形对像素中心点的覆盖来决定是否对该像素点着色，这造成在几何图形的边缘出现锯齿的现象

用数学理论来解释和解决这种缺陷，涉及数字信号处理的一些理论，如采样，重建，走样等。这些技术的学习不仅有助于理解渲染过程中数字图像的生成过程，它也是计算机图形学的重点内容，例如着色器中对纹理的采样，后处理中很多都涉及走样技术等等。接下来，我们将讨论关于数字信号处理的一些理论，并解释这些理论怎样被用在计算机图形学中。