1.5 基于物理的渲染

我们已经知道了光在空中传播及与表面交互的一些度量，并且我们知道最终摄像机收集每个像素点的辐射亮度$L$，以及怎样减轻由于屏幕分辨率的限制导致采样时走样的现象。虽然这一切建立在物体表面为理想光滑平面的基础之上，但是我们通过这样简化的模型很好地讨论了计算机图像渲染的逻辑和过程。当物体表面变得复杂时，渲染方程的计算将发生变化，但是这个逻辑框架是不会变化的。所以在理解了这些渲染过程及逻辑之后，本节就开始讨论实际渲染中，光与表面交互更复杂的情形，这也是计算机图形学关于渲染部分最需要关心的重要知识。

本节我们将建立这些光与表面复杂交互过程的数学模型，各种渲染方法的实现基本上都是基于这些光照数学模型的。当然不同级别的引擎对这些数学模型有不同级别的近似，在光传输过程中的各个环节也可能使用不同的近似方法处理（正如本书将介绍的各种全局光照算法），但是本节介绍的基础知识几乎是所有全局光照模型的基础。

由于渲染方程的复杂性，以及硬件性能的限制，早期的工业运用中（甚至处于离线渲染的电影行业）大都使用一些非常近似的模型，这些模型能够产生比较理想的效果，然而这些图像结果却不是物理上正确的。所谓物理上正确的，主要指光在场景中的传输保持能量守恒（本节后面将会讲述更多关于基于物理渲染的特征）。基于物理的渲染能够使渲染结果更能够接近物理世界的品质。

自从2012年Burley的论文[cite a:PhysicallyBasedShadingatDisney]之后，游戏行业已经开始广泛采用基于物理的渲染，并在之后几年的各种技术会议上，业界各大主流游戏引擎都纷纷展示了它们基于物理渲染的效果和品质。所以本书中大多数解决方案都是基于物理的。

双向反射分布函数

当一个表面绝对光滑时，一束入射光将按照反射定律在相应的方向上被反射，以及按照折射定律在相应的方向上被折射。对于除这两个方向以外的方向，将得不到任何来自这束入射光的光照。

我们的世界显然不是这样的，每种物体表面都有着各种不同的粗糙度，这使得光线照射到一个表面后，可以沿着不同的方向看到这些反射或折射的光。这是由于在物理世界中，每个光子入射到一个特定的微观表面上，这些微观表面由于材质的粗糙度而朝向多个不同的方向，在这个微观表面上，光与物体的交互仍然遵循反射定律和折射定律。

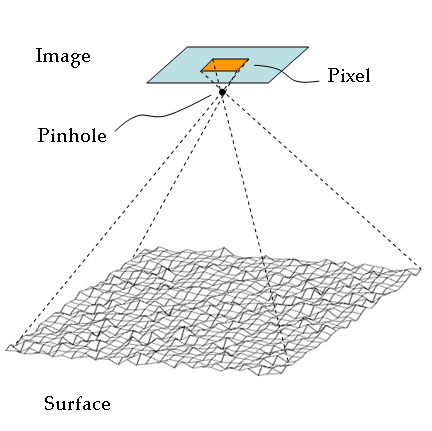
图（1）：在数字图像的世界，每一个像素点其实对应着具有不同粗糙度的表面，这个表面位于微观尺寸，它小于一个像素的尺寸，但是大于光的波长，但这个尺寸我们很难通过几何模型来模拟（图片来自Wikipedia）

然而数字图像的世界可不是这样，由于物理世界被像素化为一个离散的数字图像，一方面对于小于一个像素的微观尺寸，我们通常无法用一种真实的几何模型表述其微观结构,如图（1）所示；另一方面，即使对于宏观的尺寸，对于较远的场景，一片较大的区域将被投射到一个单一的像素点上，而这片较大的区域拥有不同的粗糙度，使得摄像机可以从各个不同的角度看见它。

那么我们怎样表示不同物体表面的这种粗糙度性质呢？首先我们从结果上来分析，由于这种微观结构的存在，它使得来自每个方向的每束光在表面的各个方向上具有一个特定的分布函数（回想第[ref sec:intro-materials]节中讲述材质时物体微观结构上的粗糙度使得一束光在一个像素点上可以沿多个不同的方向折射或反射），这个分布函数可能由多种不同的因素决定，例如粗糙度，是否是金属结构等等，但是只要找到这个分布函数，便能够有效地计算光与表面的交互。

在数学上，用一个双向反射分布函数（bidirectional reflectance distribution function，BRDF）[cite a:DirectionalReflectanceandEmissivityofanOpaqueSurface]来表示物体表面的反射。它表示反射方向上的辐射亮度增量与入射方向辐射照度增量的比率：

$$f_r(\omega_i,\omega_r)= \cfrac{{\rm d}L_r(\omega_r)}{{\rm d}E_i(\omega_i)}= \cfrac{{\rm d}L_r(\omega_r)}{L_i(\omega_i)\cos\theta_i {\rm d}\omega_i}$$

（式1）

其中，$\omega_i$是入射光方向，$\omega_r$表示观察方向，$\theta_i$为入射光方向与表面法线$\mathbf{n}$的夹角 如图（2）所示。由于在球面坐标系中，一个方向可以用一个方位角（azimuth angle）$\phi$和一个天顶角（zenith angle）$\theta$表示，因此整个BRDF函数具有4个变量。BRDF函数的单位为$sr^{-1}$，其中$sr$为立体角。直观上讲，BRDF的值表示入射光方向单位立体角的能量在反射方向上反射的比率。

图（2）：BRDF函数由2个方向组成，具有4个变量，它本质上指明了每个方向的入射光在各个方向上的反射光分布

这里使用微分方程的原因是，对于非${\rm d}\omega_i$方向的辐射照度，其与$f_r(\omega_i,\omega_r)$无关，但是仍然可能影响$L_r(\omega_r)$的值，然而${\rm d}E_i(\omega_i)$只影响${\rm d}L_r(\omega_r)$的值。即整个$L_r(\omega_r)$是由各个入射方向的光照反射的结果。

所以，给定BRDF函数，便可以求出该点处沿观察方向的辐射亮度，其值为入射方向的辐射亮度乘以BRDF函数，再乘以一个余弦因子之后，沿该点法线方向半空间的积分，即：

$$L_r(\omega_r)={\rm \int}_{\Omega}f_r(\omega_i,\omega_r)\otimes L_i(\omega_i)\cos\theta_i {\rm d}\omega_i$$

（式2）

其中$\otimes$标记表示按RGB分量相乘，因为辐射照度$E$和辐射亮度$L$都是RGB矢量，所有$f_r$仍然表示为一个由RGB三个分量构成的矢量。方程（2）又称为反射方程（reflectance equation）。

双向表面散射反射分布函数

在第【ref sec:intro-materials】节讨论材质时讲过，对于非金属不透明（透明物体由于物体内部材质连续，光折射后在物体内部的传播方向不受改变，然后从物体表面的相反方向射出。）物体，当光进入物体内部（而不仅仅是表面）时，这些折射的光会由于物体内部结构的不连续导致光沿着不同的方向继续散射，最终一部分光会被吸收，而剩下的光会从表面的另一个不同的地方散射出来，如图（2）图所示。这种现象称为次表面散射（subsurface scattering），它使得物体的表面很浅的部分看起来具有一定的透明度，例如皮肤，塑料或纤维等。

图（3）：BRDF是BSSRDF的特殊形式，即光进入物体内部经过一定的散射或吸收，然后重新从物体表面散射出来的位置，与入射点位置之间的距离小于一个像素的尺寸（图片来自Wikipedia）

如果光进入表面的点和离开表面的点之间的距离小于一个像素的尺寸，则这种交互完全可以用BRDF来描述，然而如果这个距离大于一个像素，则需要使用一个更一般的函数表示。这个函数称为双向表面散射反射分布函数（bidirectional surface scattering reflectance distribution function，BSSRDF）[cite a:GeometricConsiderationsandNomenclatureforReflectance]。BSSRDF在BRDF基础上增加一个在表面上的入射点位置和一个出射点位置，所以它是一个8维的方程，即：$f_r(\mathbf{x}_i,\omega_i,\mathbf{x}_r,\omega_r)$。

BRDF性质

物理定理赋予BRDF两个特殊的性质，第一个性质称为赫姆霍兹互反律(Helmholtz reciprocity)，它说明BRDF的入射方向和出射方向可以互相对换，其值保持不变，即：

$$f_r(\omega_i,\omega_r)=f_i(\omega_r,\omega_i)$$

（式3）

第二个性质是能量守恒（energy conservation），即所有反射的能量不能大于所有吸收的能量（不包括物体自发光的情形），这可以表示为:

$${\rm \int}_{\Omega}f_r(\omega_i,\omega_r)\cos\theta_i {\rm d}\omega_i \leq 1,\forall\omega_r$$

（式4）

式（4）表示对于一个给定的入射方向$\omega_r$，其所有出射方向的BRDF积分的值小于1，这相当于针对该入射光照的出射度$B$。可以用另一个更一般的名字来代替这个函数，即有向半球面反射（directional-hemispherical reflectance），$R(\omega_r)$:

$$R(\omega_r)= \cfrac{{\rm d}B}{{\rm d}E(\omega_r)}={\rm \int}_{\Omega}f_r(\omega_i,\omega_r)\cos\theta_i {\rm d}\omega_i$$

（式5）

$R(\omega_r)$是一个一维函数，它的变量表示入射方向。$R(\omega_r)$的值必须介于0和1之间，当值为0时表示入射的光照全部被吸收，例如金属材料；如果所有的光照都被反射，其值为1。因为其值介于0和1之间，且包含RGB三个分量，所以$R(\omega_r)$也可以表示为一个颜色值。

当然在实时渲染中，这两种性质都不是绝对遵守的。因为通常绝对遵循物理规律的BRDF函数非常复杂，实际渲染中都是采取某种近似的方法，这些不同的近似方法形成不同的BRDF模型，我们将在本章后面详细讨论它们。

BRDF可视化

因为BRDF遵循物理定律，所以使用BRDF模型来计算光与表面交互的渲染技术通常又称为基于物理的着色（physically based shading），为了更好地设计和验证不同的BRDF模型，我们需要十分便利的可视化方式使得BRDF更直观，如图（4）所示。

图（4）：几种不同的BRDF模型的可视化，一个表面通常同时包含漫反射和光泽反射，其中圆球部分为漫反射BRDF，而叶形状部分为光泽BRDF (图片来自[citem:BRDFExplorer})

由于物体表面微观结构不是绝对光滑的，这导致表面上的每个点反射或折射光（这里的入射光实际上是一个物体表面一个像素尺寸大小的范围内接收的来自某个方向的所有光线，实际上是微观上的多条光线。）至多个不同的方向（每个方向一条光线）。所以给定一个入射方向，BRDF的值分布在所有可能的出射方向上。在图（4）中，球面的部分是漫反射，因为漫反射可能沿所有出射方向都有反射光；叶形状部分则是光泽反射部分。

Disney提供有一个开源的BRDF工具（BRDF Explorer[cite m:BRDFExplorer]），它可以导入并绘制给定的BRDF模型，这些BRDF模型可以由OpenGL GLSL着色语言编写，或者来自MERL数据库的对真实材质测量的BRDF二进制数据，以及MIT CSAIL的各向异性BRDF数据格式。当参数改变时，环境可以被实时地重新渲染，可以非常方便地用来分析和评估不同的BRDF模型。

菲涅耳公式

在开始讨论BRDF模型之前，还剩下一个疑问没有解决，当光由一种介质进入另一种不同的介质，在光滑的表面发生反射和折射时，入射光被反射和折射的比率分别应该是多少呢？

这个反射和折射比率由菲涅耳方程（Fresnel equation）描述，它由菲涅耳（Augustin-Jean Fresnel）于1823年根据他的光的弹性理论提出。菲涅耳公式仅取决于入射角$\theta_i$以及两种介质的折射系数，通常用$R_F$表示菲涅尔反射率（Fresnel reflectance）。根据能量守恒定律，则折射的辐射能量比率为$1-R_F$，然而由于其折射形成的立体角的大小有所改变，因此辐射亮度的折射率却不是$1-R_F$，以下证明过程来自[cite a:ReflectionandtransmissionoflightbyaflatinterfaceFresnelsformulae]。

图5：入射光，反射光以及折射光在两种不同介质物体的辐射亮度$L$，其中$n_2>n_1$

考虑如图（5），入射辐射亮度$L_1$定义为辐射通量${\rm d}^{2}\Phi_1(\theta_1,\varphi_1)$从方向$(\theta_1,\varphi_1)$穿过无限小立体角${\rm d}\omega_1=\sin\theta_1 {\rm d}\theta_1 {\rm d}\varphi_1$，照射到面积为${\rm d}s$大小的区域的能量，即：

$$L_1= \cfrac{{\rm d}^{2}\Phi_1(\theta_1,\varphi_1)}{{\rm d}s\cos\theta_1 \sin\theta_1 {\rm d}\theta_1 {\rm d}\varphi_1}$$

（式6）

上式的分母表示入射“光锥”的几何范围，因为反射光$L_R$具有与入射光一样大小的反射角，所以它同样具有一样大小的几何范围。因此反射辐射亮度$L_R$可以表示为：

$$L_R=R_F(\theta_1)L_1$$

（式7）

对于折射“光锥”，由于折射角和入射角之间满足折射定律，通过对折射公式[ref eq:intro-snell-Law]求微分得：

$$n_1 \cos\theta_1 {\rm d}\theta_1=n_2 \cos\theta_2 {\rm d}\theta_2$$

（式8）

因为在球面坐标系统中，一个方向可以由方位角（azimuth angle），$\varphi$和天顶角（zenith angle），$\theta$组成，虽然折射导致入射角和折射角的天顶角的变化范围不一致，但是方位角的变化范围为$\pi$是相同的，入射角的方位角的变化将会导致折射角方位角相同的变化，即${\rm d}\varphi_1={\rm d}\varphi_2$。所以用折射定律的等式分别乘以式（8），再乘以${\rm d}s$得：

$$n^{2}_1{\rm d}s\cos\theta_1 \sin\theta_1 {\rm d}\theta_1 {\rm d}\varphi_1=n^{2}_2 {\rm d}s \cos\theta_2 \sin\theta_2 {\rm d}\theta_2 {\rm d}\varphi_2$$

（式9）

用${\rm d}G_1$和${\rm d}G_2$分别表示入射光锥和折射光锥的几何范围，则上式可以简化为：

$$n^{2}_1 {\rm d}G_1=n^{2}_2 {\rm d}G_2$$

（式10）

在上式中，当入射光由介质$i$进入介质$j$时，其几何范围被乘以一个因子$(n_j/n_i)^2$，但是量$n^2_i{\rm d}G_i$保持不变。这种变化从几何上也好理解，由于折射导致折射角的变化范围小于$90^{\circ}$，所以其折射方向的几何范围变小了。

由此可以推出折射后的辐射亮度为：

$$L_2=(1-R_F(\theta_1)) \cfrac{n^2_2}{n^2_1}L_1$$

（式11）

菲涅耳反射率对于金属和非金属的函数曲线有较大的不同，如图（6）所示，菲涅耳反射率对金属的影响较为微妙，对于铝，反射率几乎在$86\%$以上；对于绝缘体，菲涅耳反射率的影响则非常大，它对于大部分入射方向其反射率仅为$4\%$左右，而当几乎水平于表面方向时，它的反射率几乎为$100\%$。这种菲涅耳效应（Fresnel effect）也可以通过图（7）看出。

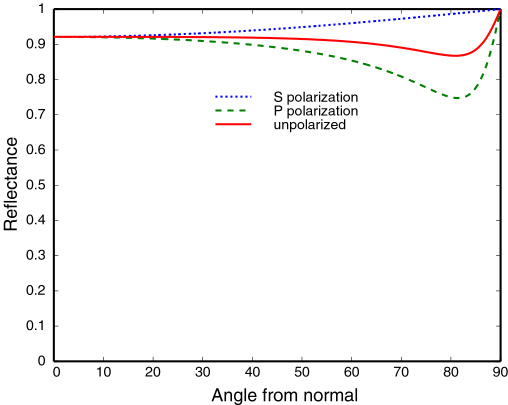
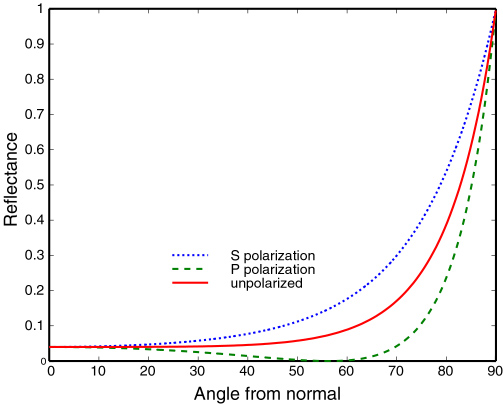
图（6）：菲涅耳反射率对金属的影响很小，对非金属的影响则很大，图中的观察角度从法线方向开始 (图片来自Stephen H. Westin swestin@earthlink.net)

需要注意的是，图（6）的虚线部分表示偏振效应，在电磁学中一个矢量场可以分解为平行于入射面和垂直于入射面的两个分量。其中对于P，即平行于入射面的分量，它入射角接近$57^{\circ}$时，所有的反射光完全被偏振，此时反射光线和折射光线相互垂直，这也叫做起偏角或者布儒斯特角（Brewster angle）。这就是为什么太阳镜可以减少接近水平方向非金属的反射强光。在计算机图形学中，我们通常忽略偏振，而取两个偏振分量的平均值。

图（7）：生活中的菲涅耳效应 (By tanakawho from Tokyo, Japan - Hospital corridor 2, CC BY 2.0, https://commons.wikimedia.org/w/index.php?curid=2138545)

由图（6）可知，菲涅耳公式的曲线非常复杂，在渲染领域我们通常不会使用原始的菲涅耳公式，[cite a:AnInexpensiveBRDFModelforPhysically-BasedRendering]于1994年提出了一种比较简单且相对比较精确的模型，他的近似方程如下：

$$R_F(\theta_i)\approx R_F(0^o)+(1-R_F(0^o))(1-\overline{\cos}\theta_i)^5$$

（式12）

其中$R_F(0^o)$表示入射光垂直于表面时的菲涅耳反射率的值。当使用Schlick近似时，只有$R_F(0^o)$一个参数，而我们可以在现实生活中找到大量物质的$R_F(0^o)$值。此外，$R_F(0^o)$的值也可以通过材质的折射率得出：

$$R_F(0^o)=( \cfrac{n_1-n_2}{n_1+n_2})^2$$

（式13）

由于介质参数是随着波谱变化的，所以菲涅耳反射率是一个光谱度量，即它包含RGB三个分量值。因为菲涅耳反射率在大部分范围内趋近于$R_F(0^o)$，因此我们也称其为材质的特征镜面反射率（characteristic specular reflectance），同时因为它满足一个颜色值的条件--具有RGB分量并且每个分量的值位于0和1之间，所以我们通常也称它为镜面颜色（specular color），通常表示为$\mathbf{c}_{spec}$，我们还将在后面的材质模型一节中介绍它。

微面元理论

本节将开始介绍BRDF模型，虽然有很多非常流行且比较理想的一些经验BRDF模型（例如[cite a:AComparisonofFourBRDFModels,a:ExperimentalAnalysisofBRDFModels,a:AnOverviewofBRDFModels]讨论了很多比较主流的BRDF模型，特别是[cite a:AnOverviewofBRDFModels]讨论了不同BRDF的分类），然而当前主流的游戏引擎[cite a:RealShadinginUnrealEngine4,a:MovingFrostbitetoPBR,a:PhysicallyBasedShadingatDisney,a:PhysicallyBasedShadinginUnity]都在采用基于微面元理论的BRDF模型，所以本书我们将只讨论这种BRDF模型。

在前面介绍材质相关内容时（第[ref sec:intro-materials]节），我们看到绝大多数物质在低于一个像素的观察尺度上，都不是绝对光滑的，称这个尺度为微观尺度（microscale）。在这个尺度下，一个像素接收到来自某个方向的光照并不是一单束光，由于一个像素的尺寸远大于光子的尺寸，因此入射光实际上是很多束光，这些光与微观上具有不同方向法线的微面元发生交互，从而反射或折射至不同的方向，如图（8）所示。

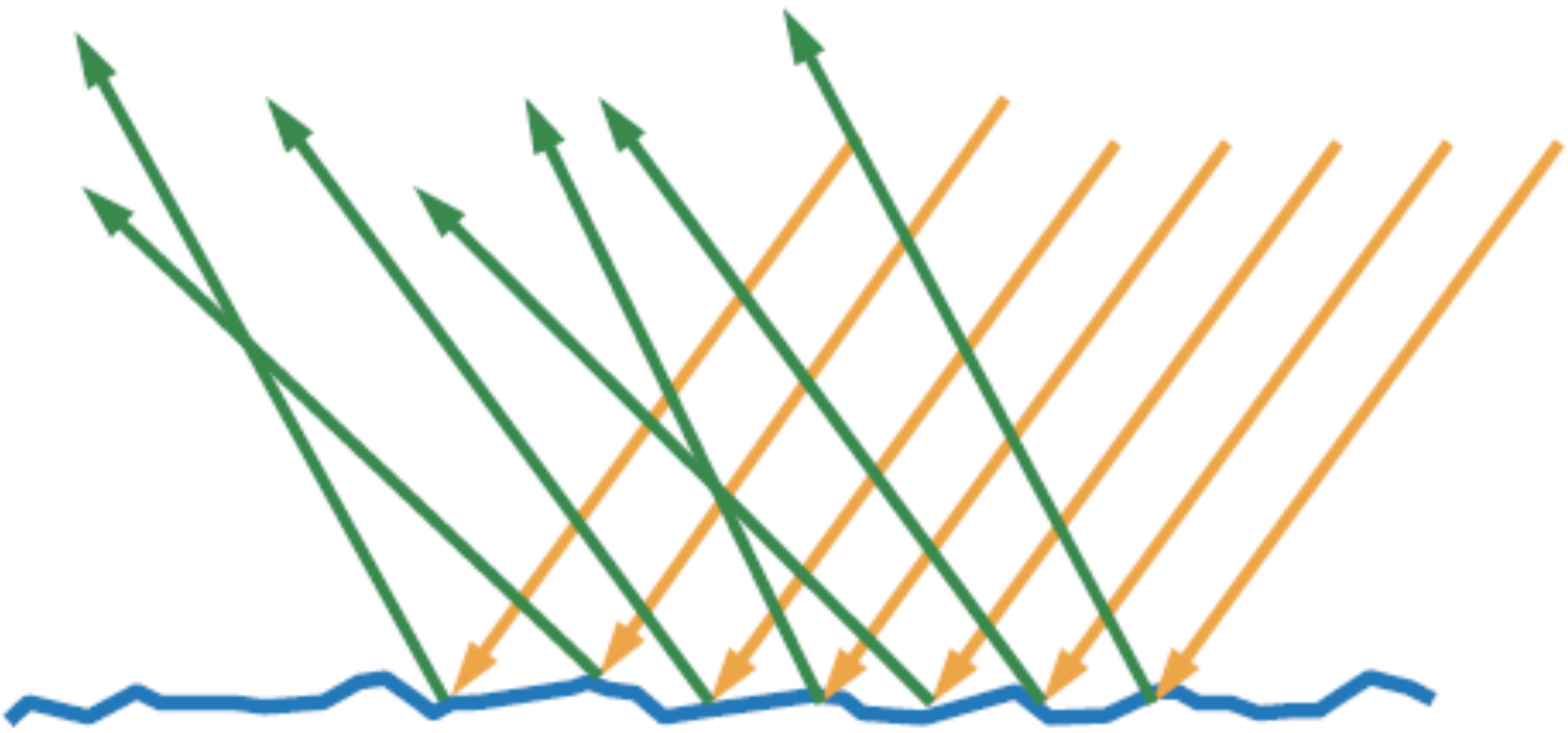
图（8）：微面元理论假设物质表面由大量微观结构的面元组成，这些微观结构远小于一个像素的尺寸，光束与每个面元进行交互将光反射或折射至不同的方向

由于这种微观结构不能通过分析的方式精确模拟，因此只能通过统计的方式来模拟这种微观结构的分布。微面元理论正是基于这样的假设，它假设物质由大量微观几何（microgeometry）结构的微面元（microfacet）组成，每个面元是绝对光滑的，因此光与这些面元的交互遵循反射定律和折射定律；而这些微面元法线（microfacet normals）方向的分布使用一个统计的法线分布函数（normal distribution function，NDF）给出，这个分布函数反应光从每个方向反射的概率，例如大多数表面的NDF函数分布集中在表面的宏观法线方向上（即通过贴图或者顶点插值记录的每个像素的法线$\mathbf{n}$）。

因为每个面元都是绝对光滑的，每束光仅在沿反射定律决定的方向上才能反射，即意味着只有那些满足反射方向刚好在观察方向$\mathbf{v}$的面元才能被看到，如图（9）所示。这意味着这些可以被观察到的面元的法线正好位于入射方向$\mathbf{l}$和观察方向$\mathbf{v}$的中间，这个矢量称为半矢量(half vector)$\mathbf{h}= \cfrac{\mathbf{l}+\mathbf{v}}{|\mathbf{l}+\mathbf{v}|}$。

图（9）：在所有微观面元中，仅仅只有红色的面元，即那些法线刚好在半矢量$\mathbf{h}$方向的面元才能被观察到（图片来自[citeb:rtr]）

并不是所有法线在半矢量$\mathbf{h}$方向的面元都会被观察到，其中的一些会在光源方向或观察方向上被其他面元阻挡，如图（10）(a)和(b)所示。尽管实际这些被阻挡的光线会继续与其他面元进行多次反射最终仍有可能进入观察视线内，如图（10）(c)所示，但是微面元理论一般忽略这种复杂的情况，即不考虑所有被阻挡的光线，本书介绍的微面元BRDF都是只考虑光的一次反射，对于在微面元之间多次反射的情形，感兴趣的读者可以参考[cite a:MultidimensionalBinarySearchTreesUsedforAssociativeSearching]。

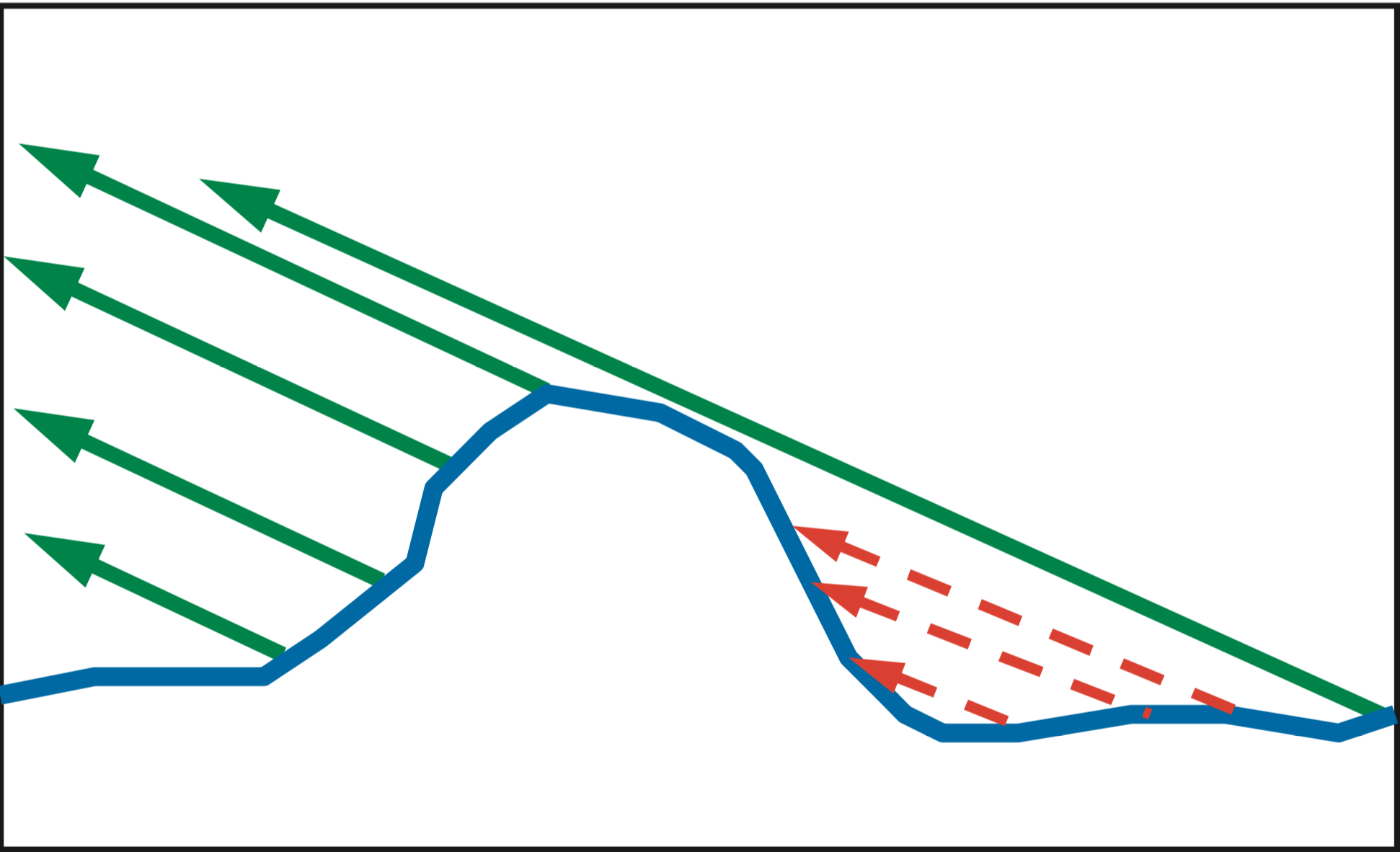
图（10）：微观面元的交互现象 (a): 黑色虚线部分表示入射光被阻挡处于阴影区，(b): 红色虚线部分表示该区域的面元在观察方向被近处的面元阻挡，(c): 光线在微观面元之间多次反射（图片来自[citeb:rtr}）

由于不考虑微观面元内部的相互反射，所以基于微面元理论的BRDF模型一般只针对光泽部分，所以它通常还需要配合一个漫反射的BRDF分布。因为漫反射主要是光线在微观结构内部经过多次反射的结果，它的光照相对于只考虑一次反射的光照要弱得多。

综合以上这些假设和理论，基于微面元理论的BRDF模型主要由两部分因素决定，即：

• 一个关于所有微观面元的表面法线分布函数$D$，其中只有法线指向半矢量$\mathbf{h}$方向的面元才会被观察到。
• 同时，对法线方向处于半矢量$\mathbf{h}$的微观面元，当且仅当它们在入射方向和观察方向没有被其他面元阻挡才能被观察到，这需要一个表示几何遮挡关系的函数$G$。

根据以上结论，再结合菲涅耳公式，对于各向同性(isotropic)材质的BRDF模型由以下式给出：

$$f(\mathbf{l},\mathbf{v})=f_d+ \cfrac{R_F(\theta_h)G(\theta_l,\theta_v)D(\theta_h)}{4\cos\theta_l \cos\theta_v}$$

（式14）

这个方程包含漫反射和光泽部分，其中漫反射通常与方向无关，为一个常数；而光泽部分包含三个组件：菲涅耳反射率$R_F(\theta_h)$，表示几何遮挡关系的$G(\theta_l,\theta_v)$，以及微面元法线分布函数$D(\theta_h)$，其中$D(\theta_h)$必须是归一化的。$\theta_l$和$\theta_v$分别表示入射方向$\mathbf{l}$和观察方向$\mathbf{v}$与表面法线$\mathbf{n}$的夹角，$\theta_h$是表面法线$\mathbf{n}$和半矢量$\mathbf{h}$之间的夹角，$\theta_d$则是入射方向$\mathbf{l}$和半矢量$\mathbf{h}$之间的夹角。由于假设材质是各项同性（我们将在后面讨论各向异性材质的法线分布函数）的，因此微面元法线分布函数$D$仅有一个变量$\theta_h$。分母$4\cos\theta_l \cos\theta_v$表示一个从微观面元空间向宏观像素空间转变的转换因子，因为$f(\mathbf{l},\mathbf{v})$是宏观空间的一个度量。

以下我们分别讨论微面元BRDF的各个部分，以及各个部分的选择，尤其我们要讨论几个主流游戏引擎各自的选择，这些选择大都基于或者源自[cite a:PhysicallyBasedShadingatDisney]的BRDF模型。首先对于菲涅耳反射率，工业中比较广泛的解决方案还是前面讲述的Schlick近似，所以本节将集中讨论法线分布函数$D$以及几何遮挡函数$G$。

微观面元法线分布函数$D$

微面元BRDF最重要的部分就是微观面元的法线分布函数NDF，它是表面的微观几何结构中，所有微观面元的法线面向不同方向的概率，它决定了光泽部分的宽度，形状及其他特征。工业中比较流行的NDF包括Beckmann[cite a:TheScatteringofElectromagneticWavesfromRoughSurfaces]，Phong[cite a:IlluminationforComputerGeneratedPictures]以及GGX [citea:Microfacetmodelsforrefractionthroughroughsurfaces]等分布函数。本节的重点不在于分析这些不同的模型，我们只需要了解不同模型的特征，以及它怎样被使用在微面元BRDF中。

根据概率的特征，$D$函数通常在其作用域（这里的作用域其实是NDF分布曲线空间）归一化为1，即：

$${\rm \int}_\Omega D(\theta_h)\cos\theta_h {\rm d}\omega =1$$

（式15）

根据微面元理论的假设，这个法线分布函数是由表面的粗糙度决定的，在后面的材质模型中我们用$roughness$表示这个粗糙度参数。Disney对MERL BRDF[cite a:AData-DrivenReflectanceModel]数据分析发现，关于光泽BRDF球状分布，它具有一个很长的拖尾，如图（11）所示，这个拖尾比一般的光泽模型都要长好几倍，传统的Blinn Phong和Gaussian分布都不能有效地表达这种拖尾效应。

图11：几种不同的光泽分布与MERL中铬材质的对比。左边: 光泽值随$\theta_h$角度的变化，其中黑色线表示MERL中的铬，红色线表示GGX分布($\alpha$ = 0.006)，绿色线表示Beckmann ($m$ = 0.013)分布, 蓝色线表示Blinn Phong ($n$ = 12000)分布。 右边: 点光源在MERL中的铬，GGX，Beckmann以及Phong分布下的光泽效果（图片来自[cite a:PhysicallyBasedShadingatDisney]）

MERL BRDF

MERL BRDF数据库是对一些实物的进行测量，以二进制数据的方式存储的BRDF数据，每个BRDF是一张$90\times 90\times 180$的三维数组，分别表示BRDF函数的$\theta_h$，$\theta_d$及$\phi_d$参数，其中$\theta_h$和$\phi_d$均以$1^{\circ}$为增量记录BRDF数据，而$\theta_d$则被压缩至一个更窄的光泽分布的形状空间。MERL BRDF每个文件为33M，它通常被用来分析真实物质表面的BRDF性质，以及用来验证各种BRDF模型。

为了有效表达这种拖尾效应，Disney发现只有GGX分布[cite a:Microfacetmodelsforrefractionthroughroughsurfaces]具有最长的拖尾，如图（11）所示，GGX实际上具有和Trowbridge-Reitz[cite a:Averageirregularityrepresentationofaroughrayreflection]一样的表述，它们的分布函数如下：

$$D_{TR}=c/(\alpha^2 \cos^2\theta_h +\sin^2\theta_h)^2$$

（式16）

Trowbridge和Reitz比较了其他一些分布函数，发现$D_{TR}$和[cite a:DiffuseReflectionofLightfromaMatteSurface]的分布函数具有相似的形式，但是后者的指数部分取值1，这就建议一个指数可变化的更一般的分布函数（generalized-Trowbridge-Reitz）：

$$D_{GTR}=c/(\alpha^2 \cos^2\theta_h +\sin^2\theta_h)^\lambda$$

（式17）

其中，$c$表示一个缩放常数，$\alpha$表示表面的粗糙度，它的值介于$0$和$1$之间，当$\alpha=0$时导致一个绝对光滑的分布，而$\alpha=1$表示表面绝对粗糙，所有的反射光都是漫反射光。GTR的分布曲线如图（12）所示。

图（12）：GTR指数取不同值时的分布曲线（图片来自[citea:PhysicallyBasedShadingatDisney}）

但是GGX仍然不足以捕捉更多的光泽细节。一些研究发现单一的光泽叶（specular lobe）分布通常不能精确地描述真实物质的光泽性质，因此一些研究建议对同一个表面使用多个光泽叶，例如[cite a:GlobalOptimizationforEstimatingaMultiple-LobeAnalyticalBRDF]等，但是大多数不会超过3个，一般以2个Specular lobe居多。所以Disney也采用了两个（实际上通过如图（11）所示，这种拖尾并不能通过调整一个GGX的参数使它覆盖的范围更宽来实现更长的拖尾，它的中心区域亮度非常高，而在狭长的拖尾部分亮度非常低，因此更适合用两个$D$分布函数来组合这种拖尾）GGX的组合来表述这种更长的拖尾。其中第一个GTR（称为Primary lobe）取值$\lambda=2$，它表示中心的高亮度区域，并且它用来表述金属材质的各向异性；第二个GTR（称为Secondary lobe）取值$\lambda=1$，它表示拖尾部分，具有更低的亮度，同时它仅表示各向同性的光照。

对于粗糙度，Disney选择使用$\alpha=roughness^2$以产生一个更线性的变化，这使得设计师能够更直观地调整效果。

对于各项异性（anisotropic）的法线分布函数，粗糙度将随着方位角$\phi$变化，根据[cite a:PhysicallyBasedShadingatDisney]，$\cfrac{1}{\alpha^2}$可以被$\cfrac{\cos^2\phi}{\alpha^2_x}+ \cfrac{\sin^2\phi}{\alpha^2_y}$替换，其中：

$$\begin{aligned} aspect&=\sqrt{1-0.9 anisotropic}\\ \alpha_x &=roughness^2/aspect\\ \alpha_y &=roughness^2\cdot aspect \end{aligned}$$

（式18）

这里$anisotropic$和$roughness$均为材质参数，参见后面材质模型一节的内容。

微观面元几何遮挡函数$G$

表示微观面元几何关系的$G$称为双向阴影遮挡函数（bidirectional shadowing-masking function），它描述的是那些具有半矢量法线的微观面元中，有多少比例是同时被入射方向和反射方向看见的（或者说没有被阻挡的）。因此$G$的一个特征是其值介于0和1之间：

$$0\leq G(\theta_l,\theta_v)\leq 1$$

（式19）

虽然$D$部分对整个微面元BRDF的影响是最大的（如图（13）所示，$G_1$在大部分方向值接近于1），但是$G$部分则是最复杂的，因为$G$的计算通常要依赖于法线分布函数$D$，所以在工业中都是首先从法线分布函数按史密斯阴影函数（Smith shadowing function）推导出真实的几何遮挡函数，然后再取一个近似函数，这个近似函数大都能直接通过$roughness$参数来直接计算。更多关于几何遮挡函数的资料可以参考[cite a:UnderstandingtheMaskingShadowingFunctioninMicrofacetBasedBRDFs]。

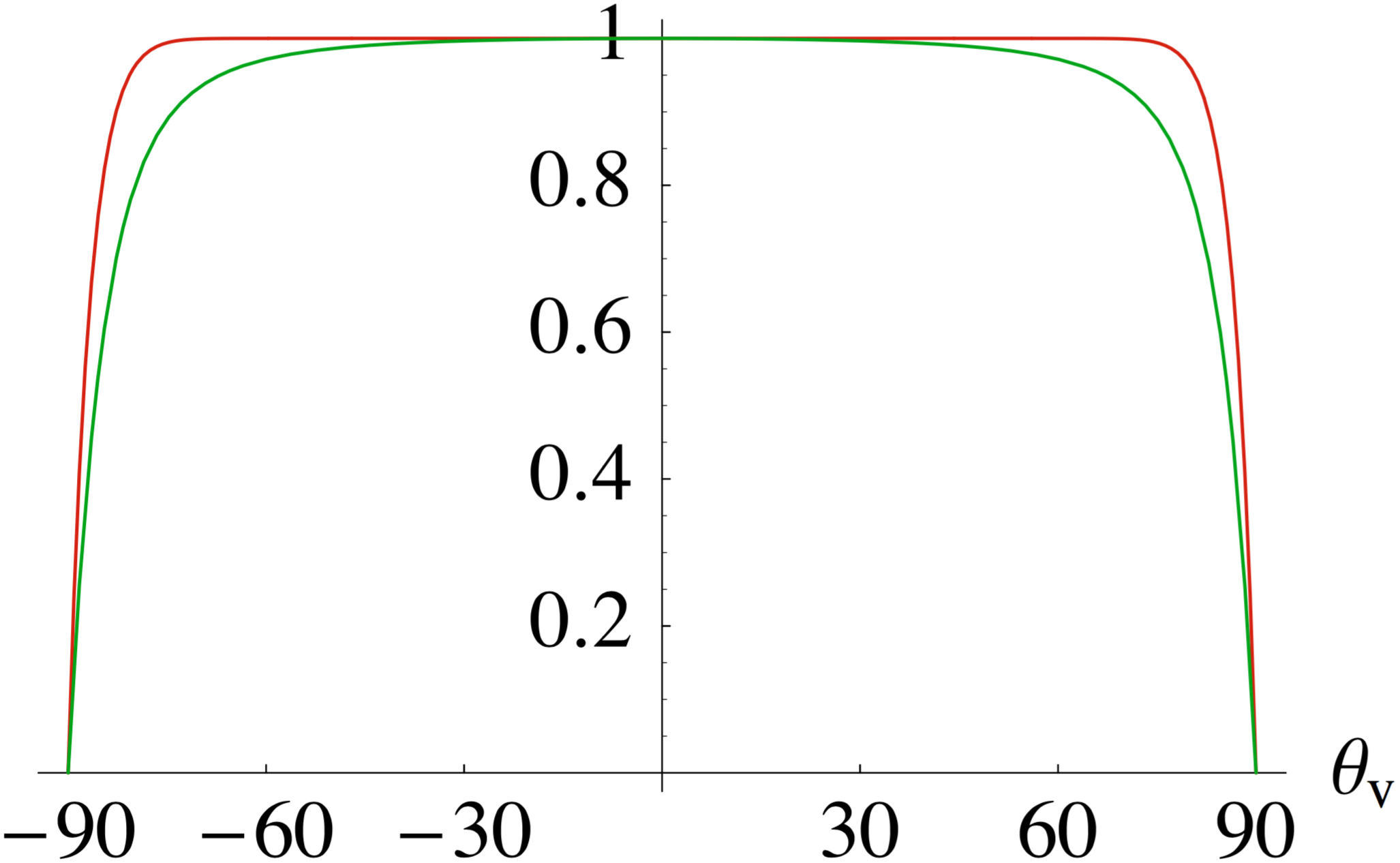
图13：S史密斯阴影函数, $G_1$，其中红色曲线基于Beckmann分布，绿色曲线基于GGX分布，由此可见$G_1$的值几乎总是接近于1，除了在接近垂直于表面法线的方向，同时GGX分布比Beckmann具有更多的阴影遮挡，这是因为其更长的拖尾导致

史密斯阴影函数

史密斯阴影函数的形式为（推导参考[cite a:UnderstandingtheMaskingShadowingFunctioninMicrofacetBasedBRDFs]）：

$$G_1(\mathbf{v},\mathbf{h})= \cfrac{\chi^{+}(\mathbf{v}\cdot\mathbf{h})}{1+\Lambda (\mathbf{v})}$$

其中，$\cfrac{1}{1+\Lambda (\mathbf{v})}$为一般化的史密斯阴影函数，$\chi^{+}(\alpha)$在$\alpha>0$时为1，$\alpha\leq 0$时为0。

请注意，史密斯阴影函数对$G$做了一个近似，即假设入射遮挡（shadowing）和出射遮挡（masking）是不相关的，所以这两部分可以分别被分离出来，并且它们都是由NDF决定的，所以具有相同的计算公式$G_1$，即：

$$G(\mathbf{v,\mathbf{l},\mathbf{h}})\approx G_1(\mathbf{v},\mathbf{h})G_1(\mathbf{l},\mathbf{h})= \cfrac{\chi^{+}(\mathbf{v}\cdot\mathbf{h})}{1+\Lambda (\mathbf{v})} \cfrac{\chi^{+}(\mathbf{l}\cdot\mathbf{h})}{1+\Lambda (\mathbf{l})}$$

（式20）

但是近年越来越多的引擎开始考虑入射遮挡和出射遮挡的相关性，因此给出更精确的几何遮挡函数，例如在[cite a:MovingFrostbitetoPBR]中：

$$G(\mathbf{v},\mathbf{l},\mathbf{h},\alpha)= \cfrac{\chi^{+}(\mathbf{v}\cdot\mathbf{h})\chi^{+}(\mathbf{l}\cdot\mathbf{h})}{1+\Lambda (\mathbf{v})+\Lambda (\mathbf{l})}$$

（式21）

其中：

$$\Lambda (\mathbf{m})= \cfrac{-1+\sqrt{1+\alpha^2 \tan^2 (\theta_m)}}{2}= \cfrac{-1+\sqrt{1+ \cfrac{\alpha^2 (1-\cos^2 (\theta_m))}{\cos^2 (\theta_m)}}}{2}$$

（式22）

在Disney的BRDF模型中，他们使用一个混合的方法，其中对Primary lobe使用Walter[cite a:Microfacetmodelsforrefractionthroughroughsurfaces]对GGX给出的近似方法：

$$G_1(\mathbf{v},\mathbf{h})=\chi^{+}( \cfrac{\mathbf{v}\cdot\mathbf{h}}{\mathbf{v}\cdot\mathbf{n}}) \cfrac{2}{1+\sqrt{1+\alpha^2_g \tan^2 \theta_v}}$$

（式23）

对于Walter的近似方法，Disney将粗糙度参数$\alpha_g$从$[0,1]$ 重映射到$[0.25,1]$，即：$\alpha_g=(0.5+roughness/2)^2$，以使$G$函数随着粗糙度变化更平滑；对于Secondary lobe，则直接使用一个固定的粗糙度参数0.25。

但是，Brent Burley在2014[cite a:ExtendingtheDisneyBRDFtoaBSDFwithIntegratedSubsurfaceScattering]年对Disney BRDF模型进行了一次修订，基于Heitz[cite a:UnderstandingtheMaskingShadowingFunctioninMicrofacetBasedBRDFs]的分析，他们去掉了这种重映射，而采用了Heitz的各项异性的形式（仅针对Primary lobe），即：

$$\Lambda (\omega_o)= \cfrac{-1+\sqrt{1+ \cfrac{1}{\alpha^2}}}{2}$$

（式24）

这里$\alpha= \cfrac{1}{\alpha_o \tan \theta_o}$，而$\alpha_o=\sqrt{\cos^2 \phi_o \alpha^2_x + \sin^2\phi_o \alpha^2_y}$。与此同时，他们考虑了入射遮挡与出射遮挡之间的相关性，使用了公式（21）而不是Smith近似（公式（21））来计算几何遮挡函数，以使在接近$90^{\circ}$的角度获得更准确的结果。

Unreal Engine 4[cite a:RealShadinginUnrealEngine4]则选择使用Schlick[cite a:AnInexpensiveBRDFModelforPhysically-BasedRendering]近似模型，并修改$k=\alpha /2$以更接近Smith GGX近似（因为Unreal Engine 4采用和Disney类似的GGX法线分布函数），同时他们仍然采样Disney对粗糙度的重映射，所以最终结果为：

$$\begin{aligned} k&= \cfrac{(roughness+1)^2}{8}\\ G_1(\mathbf{v})&= \cfrac{\mathbf{n}\cdot\mathbf{v}}{(\mathbf{n}\cdot\mathbf{v})(1-k)+k}\\ G(\mathbf{l},\mathbf{v},\mathbf{h})&=G_1(\mathbf{l})G_1(\mathbf{v}) \end{aligned}$$

（式25）

漫反射BRDF

出于性能的考虑，工业中流行的漫反射方案是朗伯BRDF（Lambert BRDF）模型，即光从各个方向以相同的亮度反射，所以BRDF函数是一个常数：

$$f_{d}(\mathbf{l},\mathbf{v})= \cfrac{\mathbf{c}_{\rm diff}}{\pi}$$

（式26）

这里$\mathbf{c}_{\rm diff}$是一个材质系数，参见后面材质模型一节的内容。

朗伯漫反射模型假设折射进入表面内部的光经历了足够多的散射，因此失去了方向性，从而在各个方向的反射率为一个常数。然而现实中的材质却很少是这样，物体微观结构导致的粗糙度不仅对光泽反射有影响，它还对对漫反射有影响，当微观面元的结构大于次表面散射的结构时，将导致一种回射反射（注意这里虽然称为反射，但它本质上是漫反射，是因为平行于光源的方向导致看见的被光源直接照射的面积增加，从而微观上漫反射的面积增加。）（retro-reflection），即光反射回到光源的方向。这种回射反射效果是因为微观面元间的遮挡导致的，如图（14）所示，当观察方向不同于光源方向，这种阻挡会大大减少被光照到面积，从而减少漫反射的面积。

图（14）：由物体微观结构的粗糙度导致的回射反射效果，这里显示的两种表面都是菲涅耳反射率很低，同时漫反射率很高的表面，所以来自表面下面的漫反射部分很重要。在左图中，观察方向接近光源方向，大部分被光照的部分同时能够被观察到，因此导致表面更亮；在右图中，观察方向大大区别于光源方向，被光源直接照射的面积大部分被阻挡，导致表面很暗（图片来自[citeb:rtr}）

回射反射对于光滑表面和粗糙表面呈现出不同的特征，首先对于比较光滑的表面（通常$f(0^{\circ})>0.5$），其光泽反射占主导，根据菲涅耳效应，其留给漫反射的光照更少，所以回射反射明显呈一个下降的趋势；而对于比较粗糙的表面($f(0^o)<0.5$)，其漫反射占据主导，所以回射反射则特别明显。

所以，Disney使用了一个新的漫反射经验模型，即：

$$f_d= \cfrac{baseColor}{\pi}(1+(F_{D90}-1)(1-\cos\theta_l)^5)(1+(F_{D90}-1)(1-\cos\theta_v)^5)$$

（式27）

这里$F_{D90}=0.5+2(roughness) \cos^2\theta_d$。对于光滑的表面，该公式可以使其漫反射的反射率最小为0.5；对于粗糙的表面，则可以最大增加到2.5倍。注意右边的因子计算两次是因为对于漫反射，光首先折射进入表面，经过一定的散射之后重新反射回原介质，所以计算两次。

材质模型

所有这些关于BRDF的计算构成后面即将讲述的渲染方程的基础，然后渲染方程被写入到着色器中，在渲染的时候GPU执行这些着色器对物体表面进行着色。也就是说，我们明白了光与表面交互的计算（BRDF），以及这种计算的表述（着色器），那么接下来的问题就是怎样表述一个表面。

不同的表面具有不同的性质，这些性质都需要以不同的方式作为参数传递给着色器，以对表面进行正确地着色。在第[ref sec:intro-materials]节我们讲过这些参数连同着色器一起都被封装到一个材质对象中，然后这些材质对象附加到不同的表面就使该表面具有对应的性质，这是材质的工作方式及过程。那么在了解具体的关于表面的交互方式（BRDF）之后，我们其实已经了解了材质需要包含的一些参数，这些不同的参数组合构成不同的材质模型（material model），本节我们分析一些材质模型当中相关的一些参数。

本节我们将以Unreal Engine 4为例来讨论材质模型的一些基本参数，Unreal Engine 4的材质模型包含大量的参数可以设置，本节我们仅讨论跟前面讲述的BRDF计算相关的参数，这称为基于物理的材质（physically based materials）[cite m:PhysicallyBasedMaterials]，其他的一些参数则会在后面的章节陆续讨论，或者你也能够从后面相关内容中去理解其他一些参数的含义及运用。在这一方面，Unreal Engine 4的材质模型是Disney[cite a:PhysicallyBasedShadingatDisney]所运用的材质模型的一个简化版本。Unreal Engine 4的材质可以通过Blueprint以可视化的方式进行编辑，如图（15）所示。

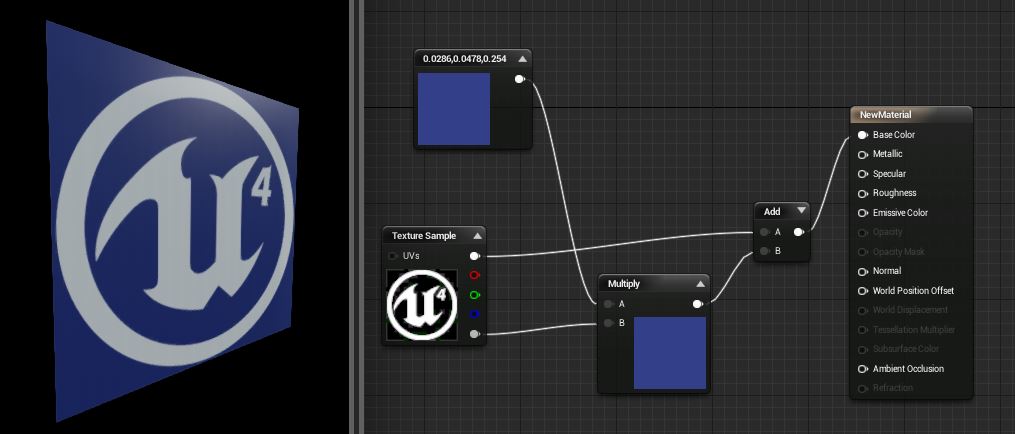
图（15）：Unreal Engine 4的材质编辑器，开发者或者美术设计师可以通过Blueprint来对材质进行编辑（图片来自Epic Games）

在Unreal Engine 4主要有4个和基于物理的渲染相关的材质参数（如图（15）中的最右边的黑色框中的参数代表Unreal Engine 4中材质的输入参数），它们分别是:

• Base Color
• Roughness
• Metallic
• Specular

所有以上这些参数的值都是介于0和1之间，例如对于Base Color而言，它是一个具有RGB三个分量的颜色值，则三个分量的取值范围都是介于0和1之间。基于物理的材质参数一般都可以通过对真实物质的测量得来。

图16：具有不同漫反射“颜色”的材质，下图表示在MERL BRDF数据库中$\phi_o=90^o$的切片（图片来自[cite a:PhysicallyBasedShadingatDisney]）

Base Color表示物体表面的真实颜色，如图（16）所示，是美术设计师在设计表面时对其绘制的实际颜色，通常使用纹理来记录一个表面各个位置的颜色值。Base Color即是方程（26）中的$\mathbf{c}_{\rm diff}$，以及方程（27）中的$baseColor$参数。

为什么$baseColor$或者$\mathbf{c}_{\rm diff}$表示物体表面的“真实颜色”？

这里我们需要理解着色的概念到底是什么，任何物体在没有光照的时候都是看不见的，可以说一个物体本身是不具备任何“颜色”的（发光的光源除外），着色的过程即是将光照射在物体表面，从而计算物体表面呈现的颜色的过程。光与物体表面进行交互分为两种方式：光泽反射和漫反射（这里仅分析绝缘体，后面会详细解释金属），对于光泽反射，它的反射率的RGB分量是一样的，即它不会改变入射光的颜色，仅改变其亮度，如表（1）所示。因此光泽反映的是光源本身，例如一个白色点光源在物体表面光泽部分看到的仍然是一个白色的（亮度被菲涅耳反射率缩放）小圆点形状，使用环境贴图作为光源则会在物体表面“印上”周围的环境。所以光泽反射几乎与物体表面的真实颜色无关。

对于漫反射部分，它指的是光折射进物体内部，在物体内部经历一定的散射后重新从表面散射回原介质中。由于这些散射回来的光丧失了方向性，所以我们用一个固定的反射常数来表示这个BRDF反射率，即是$baseColor$。所以我们所说的物体表面的“真实颜色”，其实是一个反射率，它表面当其他光照在表面进行漫反射时，在每个方向的反射率是多少，如果我们使用白色光源照亮物体表面，则物体呈现$baseColor$的颜色，使用其他颜色的光源则呈现其他不同颜色（由光源颜色与$baseColor$的乘积决定），所以$baseColor$反应的就是物体在白色光照下表面的真实颜色，如图（16）所示。

Roughness控制材质的粗糙度，越粗糙的表面，入射光越向更多的方向反射（菲涅耳反射率越低，更多光被吸收形成漫反射），物体的表面越来越接近Base Color的颜色；反之，光泽部分越来越窄，物体表面越来越光滑，高亮度的光泽使得物体表面越来越多地反射着周围的环境(或者光源的形状)，如图（17）所示。当Roughness为0时表示表面绝对光滑，成镜面反射，上图中的光源为点光源，镜面反射使得物体表面能够清楚看到点光源的形状及颜色，下图的光源为环境贴图，则光滑物体表面能够清晰地反映出周围环境；当Roughness为1时，物体表面完全漫反射，呈现Base Color的颜色。

图（17）：Unreal Engine 4中材质模型中的Roughness参数，其值从左到右由0到1变化。上图表示非金属材质，而下图表示金属材质（图片来自Epic Games）

在前面的内容中我们已经看到，Roughness参数会同时影响Specular BRDF中的NDF函数和微观面元几何遮挡函数$G$，其中在Disney的BRDF模型中，Roughness参数还会影响到漫反射BRDF，所以现在我们明白了怎样通过材质模型中一个简单的参数就能控制表面的粗糙度的计算和渲染。在有些游戏引擎中，例如Frostbite[cite a:MovingFrostbitetoPBR])，他们使用Smoothness而不是Roughness来作为表面的粗糙度参数的名字，因为更白意味着更光滑，这种理解方式更自然。

Metallic控制表面的“金属感”，金属和非金属是一个非此即彼的概念，非金属的Metallic值为0，而对于金属表面的Metallic值为1。对于纯净的物质，例如纯净的金属，石头，塑料凳，这些材质的Metallic值要么为0，要么为1。但是另一些混合物质，例如腐蚀的物体，或者布满灰尘或生锈的金属，这些材质的Metallic可能需要介于0和1之间，如图（18）所示。对于这些Metallic介于0和1之间的材质，Unreal Engine通过后面会讲述的层级纹理（layered materials）技术来实现两种材质（$Metallic=0$和$Metallic=1$）之间的混合。

图（18）：Unreal Engine 4中材质模型中的Metallic参数，其值从左到右由0到1变化，注意这时Roughness参数是没有发生变化的，所以光泽的形状不应该发生变化，左边光泽形状看起来更小，这是因为混合的原因，光泽周围亮度比较弱的拖尾的部分被混合（图片来自Epic Games）

那么Metallic参数是如何与BRDF函数发生作用的呢，在前面关于BRDF各部分的公式中似乎看不到Metallic相关的参数及其对BRDF的影响。

这里需要从前面讲述的材质分类当中去寻找答案，前面第[ref sec:intro-materials]节在讲述材质的时候说明，材质可以分为金属和非金属（或者绝缘体），而金属将折射进表面内部的光全部吸收，从而使金属材质将不会有光从表面内部再散射回来，因此金属材质没有漫反射部分。所以在Disney的BRDF模型中，他们对金属材质去掉漫反射部分，并使用Base Color的值作为光泽的入射光进行计算，不过他们仍然提供了一个$specularTint$供美术人员调整这种由入射光向$baseColor$的过度。由于这种特殊的计算方式，Metallic属性没有一个线性的计算公式，因此大部分解决方案都是使用混合的方式来实现0和1之外的插值。

对于Specular，前面我们说过，它其实等于$R_F(0^o)$的值，它表示入射光被反射的量，或者说反射率。需要注意的是，对于非金属而言，它们的反射率往往与波长无关，即它们RGB的分量相同，如表（1）所示，因此它们对于光泽的反射，仅影响入射光的亮度，而通常不会影响其颜色。但是金属的反射率通常和波长是有关的，它对入射光不同的颜色分量通常具有不同的反射率，如表（2）所示。但是传统的金属渲染使用了一种简便的方式，它直接使用$baseColor$来代替入射光，并可能与漫反射部分进行混合（$metallic$介于0和1之间时），因此$specular$通常也是一个介于0到1之间的浮点值，而不是一个颜色值。

塑料	$R_F(0^o)$	颜色
水	0.02，0.02，0.02	rgb 0.15,0.15,0.15
塑料/玻璃(较粗糙)	0.03，0.03，0.03	rgb 0.21,0.21,0.21
塑料（较光滑）	0.05，0.05，0.05	rgb 0.24,0.24,0.24
玻璃(较光滑)/红宝石	0.08，0.08，0.08	rgb 0.31,0.31,0.31
钻石	0.17，0.17，0.17	rgb 0.45,0.45,0.45

表（1）: 部分绝缘体的$R_F(0^o)$值，塑料的变化范围一般在0.03到0.05之间，玻璃具有更大的变化范围，在0.03到0.08之间，大部分绝缘体的值都在0.05附近。注意这些值都是$specular color$值，例如对于红宝石的红色，它是由于吸收进物体内部的光照的漫反射导致的，而与菲涅耳反射率无关（数据来自[citeb:rtr]）

金属	$R_F(0^o)$	颜色
金	1.00，0.71，0.29	rgb 1.00,0.86,0.57
银	0.95，0.93，0.88	rgb 0.98,0.97,0.95
铜	0.95，0.64，0.54	rgb 0.98,0.82,0.76
铁	0.56，0.57，0.58	rgb 0.77,0.78,0.78
铝	0.91，0.92，0.92	rgb 0.96,0.96,0.97
表（2）: 部分金属的$R_F(0^o)$值（数据来自[citeb:rtr]）

此外，到目前为止我们并没有看到关于介质折射率相关的参数，其实$R_F(0^o)$通常是通过介质折射率计算而出，或者通过参考真实数据，所以和折射率具有直接联系，在光照计算中直接就可以通过$R_F(0^o)$来获得介质折射率。

双向散射分布函数

前面讨论的BRDF模型通过少数几个参数就可以表述比较广泛的材质，并可以渲染出逼真的图像品质，但是对于如折射，次表面散射还是需要使用其他一些特别的(ad hoc)方法来专门处理。然而这些特别的方法通常不能保证能量守恒，因此当整个渲染器是基于光线追踪的技术来计算光照时，这种能量的不守恒将会被放大，以至于使整个图像品质失真，因为光线追踪技术对这些特别的函数进行采样，并依此在场景中通过光的传播传递能量，如果这些采样函数本身不能保证能量守恒，它将会导致这些传递的能量完全是错误的。这就是Disney在2014年开发新的基于光线追踪技术的渲染器Hyperion（关于Disney的Hyperion渲染技术，我们将在第6章详细讨论。）时遇到的困难。因此，我们需要一个对反射，折射以及次表面散射效果更统一的，并能保证能量守恒的模型。

这使我们将目光转移到更一般的双向散射分布函数（bidirectional scattering distribution function，BSDF），它其实是BRDF和BTDF的总和。BTDF全称为双向折射分布函数（bidirectional transmittance distribution function，BTDF），它和BRDF的形式基本一样，唯一的区别是BTDF的观察方向是在折射方向范围内。这样BSDF就表示，给定某点的入射方向和出射方向（在反射范围或折射范围内），出射方向上辐射亮度增量与入射方向辐射照度增量的比率。

那么BSDF包含了所有光与物体交互的计算吗？答案显然不是，由于BSDF仅考虑某一点的反射和折射，因此所有涉及距离的现象都不会覆盖到，例如光从一个点折射进入表面内部，然后经历多次散射后从另一个点重新散射回原介质的次表面散射；以及折射光在均匀介质中直线传播，经过一段距离后从物体反面的某一点折射出去的体积吸收（volumetric absorption）现象。这些现象加起来可以看做是一个一般的光与物体（而不是表面某点）交互的公式，它计算光从一个方向进入物体，在物体表面或内部经过多次折射，散射或反射之后，从物体表面的另一个点沿指定的方向散射出去。

虽然本节标题为BSDF，但是我们也会介绍后两种现象，这些内容都包含在了Disney新的光照模型当中，并且所有这些综合在一起形成一个统一的光照模型，称作集成次表面散射的Disney BSDF模型[citea:ExtendingtheDisneyBRDFtoaBSDFwithIntegratedSubsurfaceScattering]（Disney BSDF with integrated subsurface scattering）。

我们之前讨论的Disney BRDF模型本质上是一个金属和非金属的混合模型，对于Disney新的光照模型，他们仍然选择混合的方式，基于已有的BRDF模型来实现。如图（19）所示，一个新的参数$specTrans$用于控制BRDF和镜面BSDF（specular BSDF）的混合。在整个模型中，如果每个模块都是能量守恒的，那么混合后的模型也是能量守恒的。

图（19）：Disney的全新光照模型，它首先将原有的BRDF模型与新增的折射镜面BSDF模型通过参数$specTrans$混合，然后与原来的金属BRDF模型通过参数$metallic$混合

除了新增的镜面BSDF模型，Disney还加入了次表面散射模型，以及针对粗糙透明物体内折射光传播的计算，同时还包含针对超薄表面的折射处理。以下我们分别讨论这些技术。

双向折射分布函数

目前工业中比较流行的BTDF模型是Bruce Walter等[cite a:Microfacetmodelsforrefractionthroughroughsurfaces]于2007年提出的BTDF模型，本节我们首先介绍该模型及其在Disney光照模型中的使用。

Walter介绍的BTDF模型同样基于前面讨论的微面元理论，即宏观表面由多个微观面元组成，每个面元绝对光滑，光的折射遵循折射定律。假设入射光沿入射方向$\mathbf{i}$从介质折射率为$\eta_i$的介质，折射进入介质折射率为$\eta_o$的介质，经过折射后从方向$\mathbf{o}$观察。根据折射定律，$\eta_i \sin\theta_i=\eta_o \sin\theta_o$。注意折射其实仅跟两种介质折射率的比率有关，所以我们定义一个相对折射率（relative IOR）：$\eta=\eta_o/\eta_i$。

与微面元BRDF一样，Walter首先定义了一个在折射范围观察的半矢量$\mathbf{h}_t$，这里我们采用Disney使用相对折射率的方式表述：

$$\mathbf{h}_t=- \cfrac{\mathbf{i}+\eta\mathbf{o}}{|\mathbf{i}+\eta\mathbf{o}|}$$

（式28）

则Walter定义的BTDF可以写为：

$$f_t(\mathbf{i},\mathbf{o},\mathbf{n})= \cfrac{|\mathbf{i}\cdot\mathbf{h}_t|}{|\mathbf{i}\cdot\mathbf{n}|}\cdot \cfrac{|\mathbf{o}\cdot\mathbf{h}_t|}{|\mathbf{o}\cdot\mathbf{n}|}\cdot \cfrac{\eta^2}{(\mathbf{i}\cdot\mathbf{h}_t+\eta(\mathbf{o}\cdot\mathbf{h}_t))^2}\cdot (1-R_F(\mathbf{i},\mathbf{h}_t))G(\mathbf{i},\mathbf{o},\mathbf{h}_t)D(\mathbf{h}_t)$$

（式29）

折射定律不仅描述光在折射时的弯曲现象，它也间接地约束了光在折射方向发散的范围，我们在前面第[ref sec:intro-fresnel]节讲述菲涅耳公式的时候已经讨论过这种现象，即入射光的辐射亮度在折射方向被缩放$\eta^2$（即公式（11）)），$\eta^2$同样也是光束发散范围的缩放因子，如图（20）所示。

图20：根据折射定律，光束在折射后其发散范围被缩放$\cfrac{1}{\eta^2}$，其主要原因为折射定律导致出射范围变窄了

对于前面讲述的Disney BRDF模型，其菲涅耳反射率使用了Schlick近似，即：$R_{F_{Schlick}}(\theta_i)=R_F(0^o)+(1-R_F(0^o))(1-\cos\theta_i)^5$，然而它却不适用于折射，例如光从光密介质进入光疏介质时，当入射角大于临界角（critical angle），$\theta_c=\sin^{-1}\eta$时，将发生全反射，所有的光照将会反射回光密介质。

所以在Disney BSDF模型中，他们放弃了Schlick近似，而使用原始的菲涅耳公式：

$$F(\theta_i,\eta)\begin{cases} \cfrac{1}{2}\biggr[ \bigg( \cfrac{\cos\theta_i-\eta \cos\theta_t}{\cos\theta_i+\eta \cos\theta_t} \bigg)^2+\bigg( \cfrac{\cos\theta_t-\eta \cos\theta_i}{\cos\theta_t+\eta cos\theta_i} \bigg)^2 \biggr] & \cos^2\theta_t>0\\ 1 & \text{其他} \end{cases}$$

（式30）

但是对于金属BRDF，漫反射以及Secondary lobe，这些计算仍然使用Schlick近似。

体积内的吸收

对于折射光在粗糙透明物体内部的传播，根据Beer-Lambert定律，光穿过一个体积的透射比$T$为:

$$T={\rm e}^{-\sigma_{\alpha} d}$$

（式31）

这里$\sigma_\alpha$为一个吸收系数，$d$为光折射传播的距离。但是吸收系数理解起来不太直观，所以Disney使用两个新的参数：一个$transmittance$颜色值，和一个相应的$atDistance$值，并以此来推导吸收率：$\sigma_\alpha=-(\log T)/d$，如图（21）所示。

图21：在粗糙透明物体中的折射吸收，这里$transmittance$颜色值为(1,0.7,0.1), $atDistance$从左到右分别为16,8,4,2,1

我们将在第7章第[ref sec:pm-participating-media]节更详细地讨论参与介质的渲染，这里只需要了解基本概念即可。

次表面散射

2012年的Disney BRDF模型并不包括对次表面散射的计算，即光从一个点进入表面内部，经过一定散射之后从另一个点散射回原介质。但是该模型也包含了一般的漫反射之外的一些特性，这主要是前面讨论的回射反射效果。为了保留原有的部分计算方式，Disney并没有直接使用完全的BSSRDF模型替换旧的BRDF模型，而是将原有的漫反射公式拆分成两部分：一部分是与微观结构有关的具有方向性的效果（主要是回射反射），另一部分是与方向无关的一般的漫反射效果（例如Lambertian）。这样当材质次表面散射的入射点和出射点的距离小于一个像素尺寸时，还是使用原来的模型，当其大于一个像素尺寸时，则使用新的BSSRDF模型替换与方向无关的部分漫反射。

原有BRDF模型按如下的方式拆分：

$$\begin{aligned} f_d&=f_{Lambert}(1-0.5F_L)(1-0.5F_V)+f_{retro-reflection}\\ f_{Lambert}&= \cfrac{baseColor}{\pi}\\ f_{retro-reflection}&= \cfrac{baseColor}{\pi}R_R(F_L+F_V+F_LF_V(R_R-1))\\ \text{其中}&\\ F_L&=(1-\cos\theta_l)^5\\ F_V&=(1-\cos\theta_v)^5\\ R_R&=2roughness \cos^2\theta_d \end{aligned}$$

（式32）

双向表面散射反射分布函数BSSRDF通常可以表示为：

$$S(x_i,\omega_i;x_o,\omega_o)=CF_t(x_i,\omega_i)R(|x_o-x_i|)F_t(x_o,\omega_o)$$

（式33）

其中$F_t$表示菲涅耳折射率，而$R$表示一个反射配置(reflectance profile)。对于$R(r)$，目前有几种基于物理的模型，如Jensen等[citea:Apracticalmodelforsubsurfacelighttransport]的Dipole散射模型，d’Eon和Geoffrey Irving[citea:AQuantizedDiffusionModelforRenderingTranslucentMaterials]的Quantized散射模型，以及Habel等[citea:PhotonBeamDiffusion:AHybridMonteCarloMethodforSubsurfaceScattering]的Photon Beam散射模型等。这些模型都是使用基于物理的公式推导而出，相对比较复杂。Burley从Schlick对菲涅耳反射率的近似得到启发（回想图（6），菲涅耳反射率是由相互垂直的两条偏振光线的菲涅耳反射率构成，Schlick通过对曲线的观察使用两条曲线的平均值来近似菲涅耳反射率函数。），通过对基于Monte Carlo模拟（Monte Carlo方法就是对每条进入表面内部的光随机选择方向进行散射，然后从另一个点离开，通过计算经过这些路径后的结果来绘制$R(r)$函数曲线，Monte Carlo模拟将在第5章详细介绍。）的$R(r)$的分布的观察（如图（23）所示），提出使用两个指数项的和来近似$R(r)$，这样大大简化了计算，同时又达到前面几种基于物理的模型相似的结果。

在Jensen的Dipole散射模型，能量在两个点之间根据辐射度理论传递，光束在次表面的多次散射过程被使用一个简单的单次散射近似，如图（22）所示。

图（22）：Dipole散射模型使用单次散射来近似次表面散射，单次散射通常仅与两点之间的距离有关

对于这个单次散射与距离之间的关系$R(r)$，通过使用Monte Carlo模拟，Disney发现其可以使用两个指数项的和很好的近似，如图（23）所示。所以Disney使用以下函数作为其散射模型的近似配置：

图（23）：Monte Carlo散射模拟，基于指数近似的散射计算和Dipole模型的对比

$$R_d(r)= \cfrac{{\rm e}^{-r/d}+{\rm e}^{-r/(3d)}}{8\pi dr}$$

（式34）

为了计算每一束入射光对其他位置漫反射的贡献，需要针对整个无限的平面的每一个位置做一个积分计算，当对整个无限平面做积分计算时，其$R_d(r)$散射函数是归一化的，即该入射点向周围所有位置扩散的总量为1：

$${\rm \int}^{2\pi}_0{\rm \int}^\infty_0 R_{\rm d}(r)r{\rm d}r{\rm d}\phi=1$$

（式35）

因此该配置称为归一化的（从后面的内容可知，归一化的分布函数可以简单地使用Inversion Method来采样。）散射（normalized diffusion），因为其是归一化的，所以每一个点的漫反射颜色值可以通过对整个表面做积分的结果乘以$baseColor$来计算。他们通过一个参数$scatterDistance$来表示参数$d$，当$scatterDistance=0$时，直接使用原来的BRDF漫反射模型。注意，Disney的BSDF模型中可以分别对R，G和B设置不同的$scatterDistance$值，$scatterDistance$本质上控制$R(r)$曲线的高度和宽度，对于美术人员来讲，它可以理解为次表面的柔和度（softness）。如图（24）表示不同柔和度下的效果。

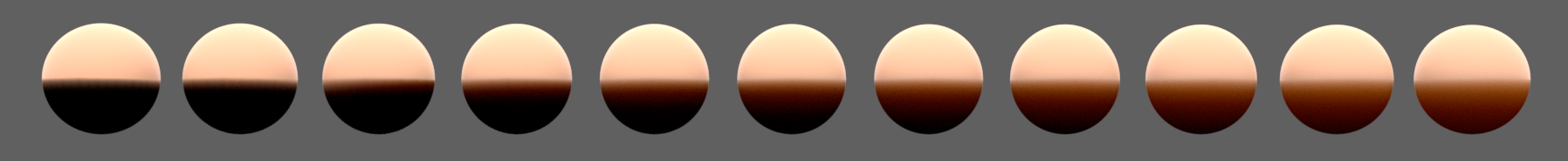
图24：对一个单位圆使用不同的$scatterDistance$值进行渲染，其值从左到右从(0.0,0.0,0.0)到(0.5,0.25,0.125)变化。这里单位圆的上半部分被火炉发出的光照射，下面为认为设置的阴影以强调阴影周围的柔和效果；注意此处左边第一个园当$scatterDistance=0$时使用原来的BRDF漫反射模型渲染，由此可以看出BRDF和BSSRDF之间能够平滑过渡

Disney的归一化散射模型在电影《超能陆战队》（Big Hero 6）中第一次使用，它用在了电影中除头发以外的所有次表面反射中。

超薄表面的渲染

对于超薄表面，Disney假设它散射的入射点和出射点位于同一点，和固体物体一样，仍然使用$specTrans$参数在完全漫反射和完全光泽（包括反射和折射）之间混合。

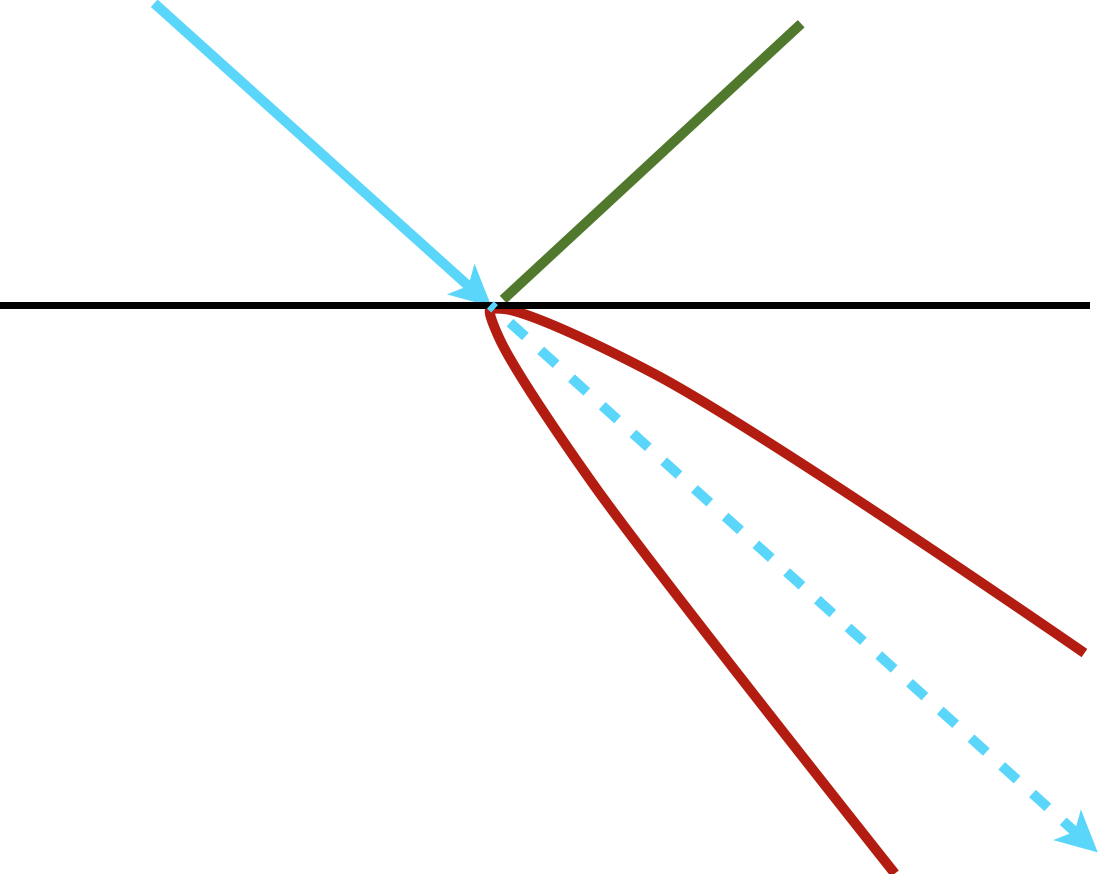
图（25）：超薄表面的折射可以近似为没有弯曲发生，这样就可以使用BRDF来计算BTDF，只不过需要反射到表面的另一边

他们观察到超薄表面发生折射时的弯曲现象可以近似地被移除，即对于折射光可以近似看做没有弯曲发生，如图（25）所示。所以镜面 BTDF部分可以通过镜面 BRDF来计算，但是反射到表面的另一边。即：

$$\begin{aligned} specular reflection &= FDG\\ specular transmission &= (1-F)DG \end{aligned}$$

（式36）

当然这样做有一个缺陷，由于折射可以放大或者缩小粗糙度，因此两边的粗糙度是不一样的，一个更好的方法是基于相对介质折射率$\eta$来缩放粗糙度，但是这样调整后的结果没有太大的变化。

对于漫反射，由于入射点和出射点之间的距离为0，因此不存在次表面散射，整个漫反射模型使用原来的BRDF模型。由于回射反射效果跟入射光有关，所以表面的反面仅有与方向无关的漫反射（Lambert部分）出现，而不包含回射反射及Sheen部分。Disney使用一个$diffTrans$参数来将漫反射从反射光一面转移到折射光一面，如图（26）所示。

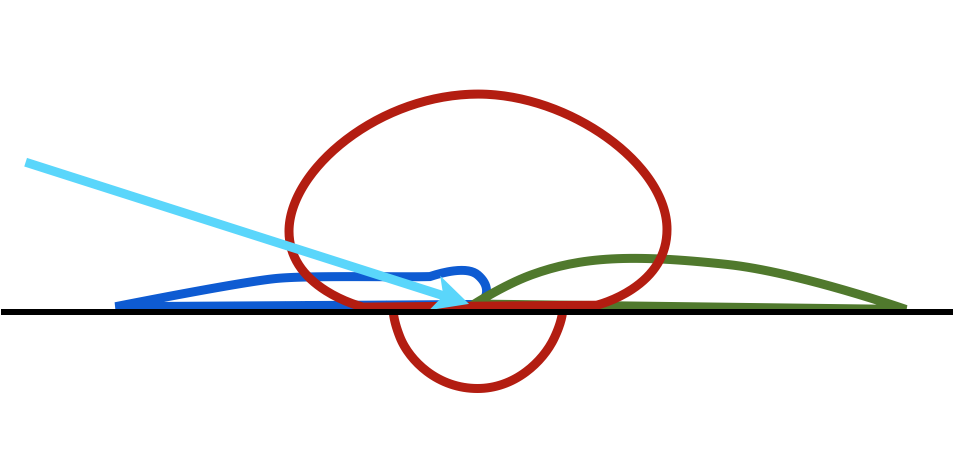
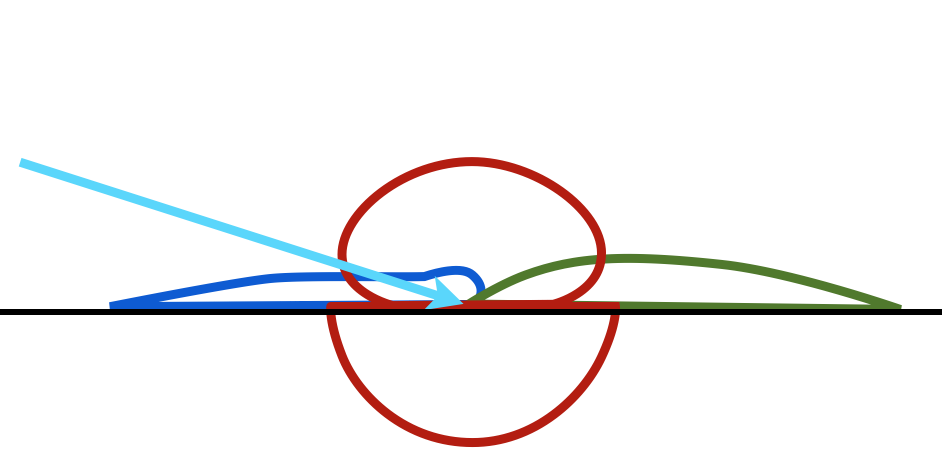
图26：$diffTrans$参数将与方向无关的漫反射部分转移到表面的反面，红色曲线表示与方向无关的漫反射，蓝色曲线表示回射反射，浅绿色表示Sheen效果

在Disney 2014年的动画电影《超能陆战队》中，角色大白(Baymax)全身使用这种超薄表面渲染技术渲染。此外，该技术还广泛运用于纸，布料，衣服等超薄材料，如图（27）所示。

图（27）：Disney 2014年动画长片《超能陆战队》，其中角色大白全身使用一种特殊的超薄表面的渲染技术（图片版权归Walt Disney Animation Studios）